PyHubWeekly

《动手学计算机视觉》从数字图像处理到深度计算机视觉，深入浅出，理论与实践相结合，让你在最短的时间内入门计算机视觉！

专注Python、AI、大数据，欢迎关注公众号七步编程！

序言
第一章数字图像处理
第二章传统目标检测
第三章卷积神经网络

序言

计算机视觉是当下最为火热的人工智能方向之一，有关计算机视觉的书籍、课程随处可见，很容易获取。

但是，目前计算机视觉方面的书籍有2个显著的痛点：

过于偏重理论
偏向深度学习

首先，过于偏重理论。目前的书籍大多是围绕向你讲解什么是CNN、图像的特征提取、模型训练是怎么样的过程。但是，该如何实现，却浅尝辄止。

往往，我们很容易理解文字语言，但是它毕竟和计算机语言有一定的差距，在模型的搭建、训练、验证过程中，会使用到很多Python、tensorflow的知识，而这些知识对于很多初学者来说同样有一定的门槛。因此，往往学习计算机视觉的过程中是隔离的，很多人知道LeNet、AlexNet等模型架构师什么样的，有哪几层网络，但是却不知道该如何实现，最终只能纸上谈兵。

其次，偏向于深度学习。学习一门知识，只有理解它的来龙去脉才能走的更远。由于深度计算机视觉这几年发展很快，仅仅学习深度计算机视觉就已经成为一项巨大挑战。因此，很多书籍和教程直接从深度计算机视觉开始讲起。

但是，计算机视觉是一个和数字图像处理密切相关的领域，它是在漫长的过程中逐渐走到今天深度计算机视觉的。只有清晰的了解图像的本质，传统机器学习是如何解决目标检测的，特征提取是怎么回事，这样才能更加有助于深入理解计算机视觉。

而本书，就从这些痛点着手，争取成为一本对计算机视觉初学者有价值的书籍。

《动手学计算机视觉》这本书的重点就是强调动手，避免纸上谈兵，每一部分知识，都会采用理论+编程的讲解方式，让你熟悉理论知识的基础上，知道如何使用，同时加深对于模型的认知。

其次，本书另外一个最大的优势就是涉及知识面广，从数字图像处理，到传统目标识别，再到卷积神经网络。这个过程中图像去噪、图像分割、HOG、DPM、Dropout、VGG等你有所耳闻的，你都会在这本书里找到想要的答案。

第一章数字图像处理

1.1 图像预处理之图像去噪

前言

很多人想入门AI，可是AI包含很多方向，我建议首先应该明确的选择一个方向，然后有目标、有针对的去学习。

计算机视觉作为目前AI领域研究较多、商业应用较为成功的一个方向，这几年也是非常火热，无论是学术界还是企业界，学术界有CVPR、ICCV、ECCV等顶刊，企业界对计算机视觉领域的人口需求也非常的大，因此，我从计算机视觉这个方向开始着手AI教程。

介绍

最近几年计算机视觉非常火，也出现了很多成熟的卷积神经网络模型，比如R-CNN系列、SSD、YOLO系列，而且，这些模型在github上也有很多不错的开源代码，所以，很多入门计算机视觉的人会早早的克隆下开源代码、利用tensorflow或pytorch搭建计算机视觉平台进行调试。

我个人不推崇这种方式，我更推崇对图像底层的技术有一些了解，比如图像去噪、图像分割等技术，这有几点好处：

对图像内部的结构有更清晰的认识
这些技术可以用于计算机视觉预处理或后处理，能够有助于提高计算机视觉模型精度

第一讲，我从图像去噪开始说起，图像去噪是指减少图像中造成的过程。现实中的图像会受到各种因素的影响而含有一定的噪声，噪声主要有以下几类：

椒盐噪声
加性噪声
乘性噪声
高斯噪声

图像去噪的方法有很多种，其中均值滤波、中值滤波等比较基础且成熟，还有一些基于数学中偏微分方程的去噪方法，此外，还有基于频域的小波去噪方法。均值滤波、中值滤波这些基础的去噪算法以其快速、稳定等特性，在项目中非常受欢迎，在很多成熟的软件或者工具包中也集成了这些算法，下面，我们就来一步一步实现以下。

编程实践

完整代码地址：
https://github.com/jakpopc/aiLearnNotes/blob/master/computer_vision/image_denoising.py
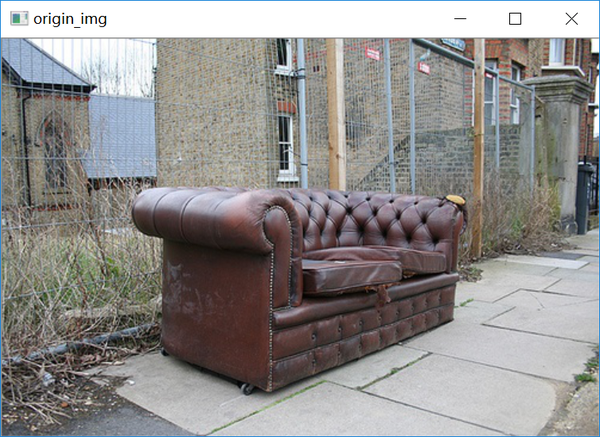
requirement:scikit-image/opencv/numpy

首先读取图像，图像来自于voc2007:

img = cv2.imread("../data/2007_001458.jpg")
cv2.imshow("origin_img", img)
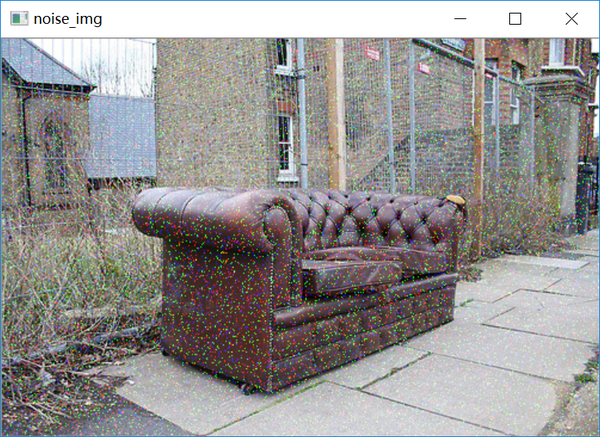
cv2.waitKey()

生成噪声图像，就是在原来图像上加上一些分布不规律的像素值，可以自己用随机数去制造噪声，在这里，就用Python第三方库scikit-image的random_noise添加噪声：

方法1：

noise_img = skimage.util.random_noise(img, mode="gaussian")

mode是可选参数：分别有'gaussian'、'localvar'、'salt'、'pepper'、's&p'、'speckle'，可以选择添加不同的噪声类型。

方法2：

也可以自己生成噪声，与原图像进行加和得到噪声图像：

def add_noise(img):
    img = np.multiply(img, 1. / 255,
                        dtype=np.float64)
    mean, var = 0, 0.01
    noise = np.random.normal(mean, var ** 0.5,
                             img.shape)
    img = convert(img, np.floating)
    out = img + noise
    return out

最后是图像去噪，图像去噪的算法有很多，有基于偏微分热传导方程的，也有基于滤波的，其中基于滤波的以其速度快、算法成熟，在很多工具包中都有实现，所以使用也就较多，常用的滤波去噪算法有以下几种：

中值滤波
均值滤波
高斯滤波

滤波的思想和这两年在计算机视觉中用的较多的卷积思想类似，都涉及窗口运算，只是卷积是用一个卷积核和图像中对应位置做卷积运算，而滤波是在窗口内做相应的操作，

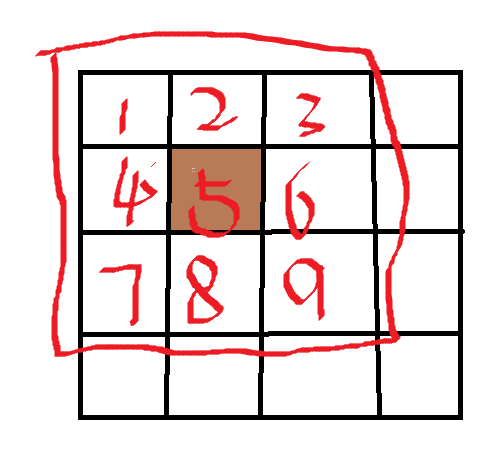
以均值滤波为例，

对图像中每个像素的像素值进行重新计算，假设窗口大小ksize=3，图像中棕色的"5"对应的像素实在33的邻域窗口内进行计算，对于均值滤波就是求33窗口内所有像素点的平均值，也就是： $$ \frac{1+2+3+4+6+7+8+9}{9}=4.4 $$ 同理，对于中值滤波就是把窗口内像素按像素值大小排序求中间值，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到，

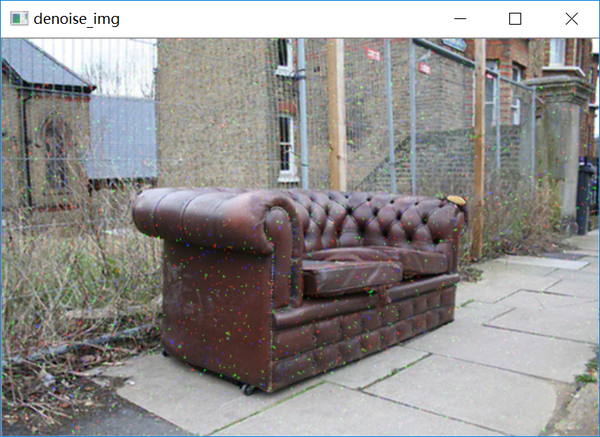
下面开始编写去噪部分的代码：

方法1：

可以使用opencv这一类工具进行去噪：

# 中值滤波
denoise = cv2.medianBlur(img, ksize=3)
# 均值滤波
denoise = cv2.fastNlMeansDenoising(img, ksize=3)
# 高斯滤波
denoise = cv2.GaussianBlur(img, ksize=3)

方法2：

编程一步一步实现图像去噪，首先是计算窗口邻域内的值，这里以计算中值为例：

def compute_pixel_value(img, i, j, ksize, channel):
    h_begin = max(0, i - ksize // 2)
    h_end = min(img.shape[0], i + ksize // 2)
    w_begin = max(0, j - ksize // 2)
    w_end = min(img.shape[1], j + ksize // 2)
    return np.median(img[h_begin:h_end, w_begin:w_end, channel])

然后是去噪部分，对每个像素使用compute_pixel_value函数计算新像素的值：

def denoise(img, ksize):
    output = np.zeros(img.shape)
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            output[i, j, 0] = compute_pixel_value(img, i, j, ksize, 0)
            output[i, j, 1] = compute_pixel_value(img, i, j, ksize, 1)
            output[i, j, 2] = compute_pixel_value(img, i, j, ksize, 2)
    return output

1.2 图像预处理之图像增强

前言

图像增强是图像处理中一种常用的技术，它的目的是增强图像中全局或局部有用的信息。合理利用图像增强技术能够针对性的增强图像中感兴趣的特征，抑制图像中不感兴趣的特征，这样能够有效的改善图像的质量，增强图像的特征。

介绍

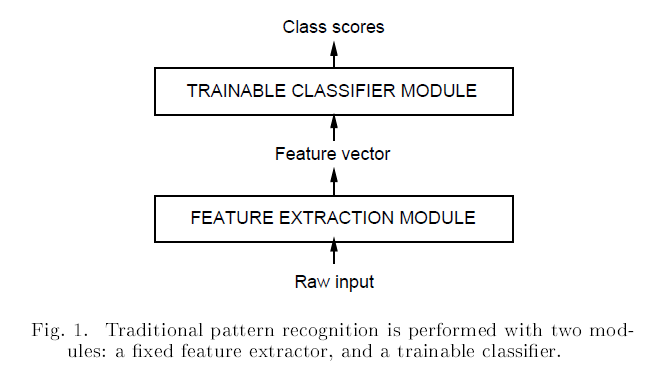
计算机视觉主要有两部分组成：

特征提取
模型训练

其中第一条特征提取在计算机视觉中占据着至关重要的位置，尤其是在传统的计算机视觉算法中，更为明显，例如比较著名的HOG、DPM等目标识别模型，主要的研究经历都是在图像特征提取方面。图像增强能够有效的增强图像中有价值的信息，改善图像质量，能够满足一些特征分析的需求，因此，可以用于计算机视觉数据预处理中，能够有效的改善图像的质量，进而提升目标识别的精度。

图像增强可以分为两类：

频域法
空间域法

首先，介绍一下频域法，顾名思义，频域法就是把图像从空域利用傅立叶、小波变换等算法把图像从空间域转化成频域，也就是把图像矩阵转化成二维信号，进而使用高通滤波或低通滤波器对信号进行过滤。采用低通滤波器（即只让低频信号通过）法，可去掉图中的噪声；采用高通滤波法，则可增强边缘等高频信号，使模糊的图片变得清晰。

其次，介绍一下空域方法，空域方法用的比较多，空域方法主要包括以下几种常用的算法：

直方图均衡化
滤波

直方图均衡化

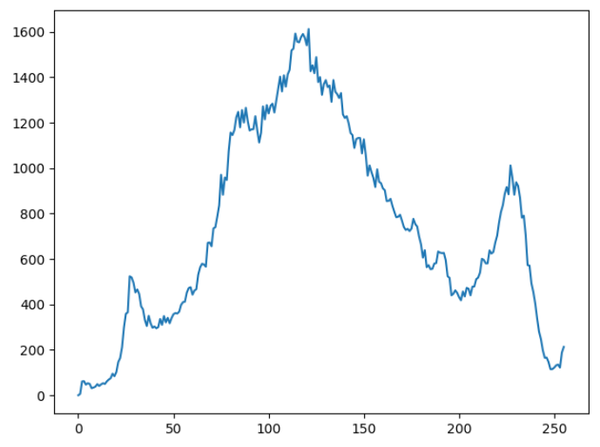
直方图均衡化的作用是图像增强，这种方法对于背景和前景都太亮或者太暗的图像非常有用。直方图是一种统计方法，根据对图像中每个像素值的概率进行统计，按照概率分布函数对图像的像素进行重新分配来达到图像拉伸的作用，将图像像素值均匀分布在最小和最大像素级之间。

具体原理和示例如下：

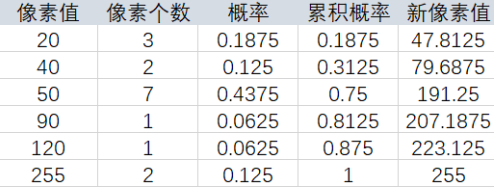
原图像向新图像的映射为： $$ s_k = \sum_{j=0}^{k}{\frac{n_j}{n}}, k=0, 1, ...,L-1 $$

其中 L 为灰度级。

用直白的语言来描述：把像素按从小到大排序，统计每个像素的概率和累计概率，然后用灰度级乘以这个累计概率就是映射后新像素的像素值。

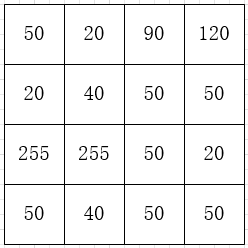
假设一幅图像像素分布如图，像素级为255，利用直方图对像素分布进行统计，示例如下：

滤波

基于滤波的算法主要包括以下几种：

均值滤波
中值滤波
高斯滤波

这些方法主要用于图像平滑和去噪，在前一讲中已经阐述，感兴趣的可以看一下【动手学计算机视觉】第一讲：图像预处理之图像去噪。

编程实践

完整代码地址： 
https://github.com/jakpopc/aiLearnNotes/blob/master/computer_vision/image_enhancement.py 
requirement:matplotlib/opencv

本文主要介绍直方图均衡化图像增强算法，前一讲已经实现了滤波法，需要的可以看一下。

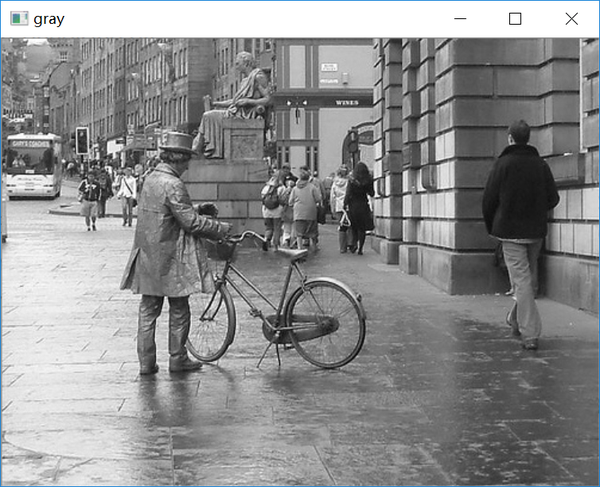
首先利用opencv读取图像并转化为灰度图，图像来自于voc2007:

img = cv2.imread("../data/2007_000793.jpg")
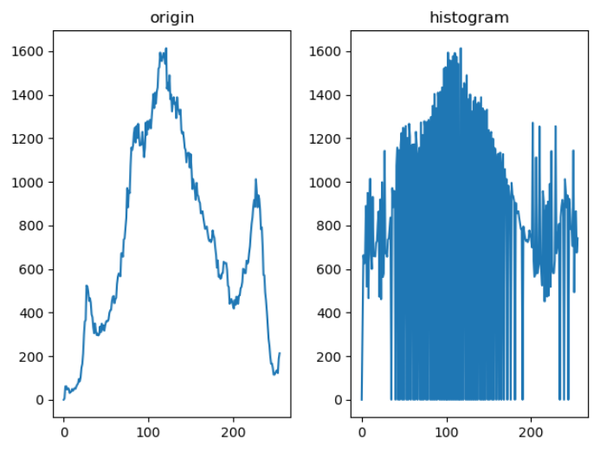
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)

可以显示图像的灰度直方图：

def histogram(gray):
    hist = cv2.calcHist([gray], [0], None, [256], [0.0, 255.0])
    plt.plot(range(len(hist)), hist)
# opencv calcHist函数传入5个参数：
# images：图像
# channels：通道
# mask：图像掩码，可以填写None
# hisSize：灰度数目
# ranges：回复分布区间

直方图均衡化，这里使用opencv提供的函数：

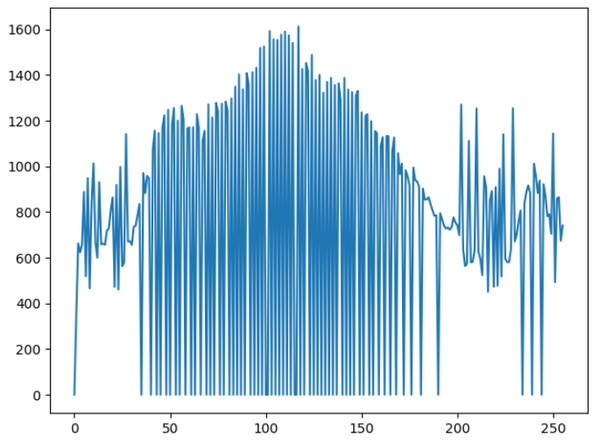
dst = cv2.equalizeHist(gray)

均衡化后的图像为：

可以从上图看得出，图像的对比度明显比原图像更加清晰。

1.3 图像预处理之图像分割

前言

图像分割是一种把图像分成若干个独立子区域的技术和过程。在图像的研究和应用中，很多时候我们关注的仅是图像中的目标或前景(其他部分称为背景)，它们对应图像中特定的、具有独特性质的区域。为了分割目标，需要将这些区域分离提取出来，在此基础上才有可能进一步利用，如进行特征提取、目标识别。因此，图像分割是由图像处理进到图像分析的关键步骤，在图像领域占据着至关重要的地位。

介绍

提到图像分割，主要包含两个方面：

非语义分割
语义分割

首先，介绍一下非语义分割。

非语义分割在图像分割中所占比重更高，目前算法也非常多，研究时间较长，而且算法也比较成熟，此类图像分割目前的算法主要有以下几种：

阈值分割

阈值分割是图像分割中应用最多的一类，该算法思想比较简单，给定输入图像一个特定阈值，如果这个阈值可以是灰度值，也可以是梯度值，如果大于这个阈值，则设定为前景像素值，如果小于这个阈值则设定为背景像素值。

阈值设置为100对图像进行分割：

区域分割

区域分割算法中比较有代表性的算法有两种：区域生长和区域分裂合并。

区域生长算法的核心思想是给定子区域一个种子像素，作为生长的起点，然后将种子像素周围邻域中与种子像素有相同或相似性质的像素(可以根据预先设定的规则，比如基于灰度差)合并到种子所在的区域中。

区域分裂合并基本上就是区域生长的逆过程，从整个图像出发，不断分裂得到各个子区域，然后再把前景区域合并，实现目标提取。

聚类

聚类是一个应用非常广泛的无监督学习算法，该算法在图像分割领域也有较多的应用。聚类的核心思想就是利用样本的相似性，把相似的像素点聚合成同一个子区域。

边缘分割

这是图像分割中较为成熟，而且较为常用的一类算法。边缘分割主要利用图像在边缘处灰度级会发生突变来对图像进行分割。常用的方法是利用差分求图像梯度，而在物体边缘处，梯度幅值会较大，所以可以利用梯度阈值进行分割，得到物体的边缘。对于阶跃状边缘，其位置对应一阶导数的极值点，对应二阶导数的过零点(零交叉点)。因此常用微分算子进行边缘检测。常用的一阶微分算子有Roberts算子、Prewitt算子和Sobel算子，二阶微分算子有Laplace算子和Kirsh算子等。由于边缘和噪声都是灰度不连续点，在频域均为高频分量，直接采用微分运算难以克服噪声的影响。因此用微分算子检测边缘前要对图像进行平滑滤波。LoG算子和Canny算子是具有平滑功能的二阶和一阶微分算子，边缘检测效果较好，因此Canny算子也是应用较多的一种边缘分割算法。

直方图

与前面提到的算法不同，直方图图像分割算法利用统计信息对图像进行分割。通过统计图像中的像素，得到图像的灰度直方图，然后在直方图的波峰和波谷是用于定位图像中的簇。

水平集

水平集方法最初由Osher和Sethian提出，目的是用于界面追踪。在90年代末期被广泛应用在各种图像领域。这一方法能够在隐式有效的应对曲线/曲面演化问题。基本思想是用一个符号函数表示演化中的轮廓（曲线或曲面），其中符号函数的零水平面对应于实际的轮廓。这样对应于轮廓运动方程，可以容易的导出隐式曲线/曲面的相似曲线流，当应用在零水平面上将会反映轮廓自身的演化。水平集方法具有许多优点：它是隐式的，参数自由的，提供了一种估计演化中的几何性质的直接方法，能够改变拓扑结构并且是本质的。

语义分割和非语义分割的共同之处都是要分割出图像中物体的边缘，但是二者也有本质的区别，用通俗的话介绍就是非语义分割只想提取物体的边缘，但是不关注目标的类别。而语义分割不仅要提取到边缘像素级别，还要知道这个目标是什么。因此，非语义分割是一种图像基础处理技术，而语义分割是一种机器视觉技术，难度也更大一些，目前比较成熟且应用广泛的语义分割算法有以下几种：

Grab cut
Mask R-CNN
U-Net
FCN
SegNet

由于篇幅有限，所以在这里就展开介绍语义分割，后期有时间会单独对某几个算法进行详细解析，本文主要介绍非语义分割算法，本文就以2015年UCLA提出的一种新型、高效的图像分割算法--相位拉伸变换为例，详细介绍一下，并从头到尾实现一遍。

相位拉伸变换

相位拉伸变换(Phase Stretch Transform, PST)，是UCLA JalaliLab于2015年提出的一种新型图像分割算法Edge Detection in Digital Images Using Dispersive Phase Stretch Transform，该算法主要有两个显著优点：

速度快
精度高
思想简单
实现容易

PST算法中，首先使用定位核对原始图像进行平滑，然后通过非线性频率相关（离散）相位操作，称为相位拉伸变换(PST)。 PST将2D相位函数应用于频域中的图像。施加到图像的相位量取决于频率;也就是说，较高的相位量被应用于图像的较高频率特征。由于图像边缘包含更高频率的特征，因此PST通过将更多相位应用于更高频率的特征来强调图像中的边缘信息。可以通过对PST输出相位图像进行阈值处理来提取图像边缘。在阈值处理之后，通过形态学操作进一步处理二值图像以找到图像边缘。思想主要包含三个步骤：

非线性相位离散化
阈值化处理
形态学运算

下面来详细介绍一下。

相位拉伸变换，核心就是一个公式，

$$ A[n, m]=\angle(IFFT2(\tilde{K}[p, q]\cdot\tilde{L}[p, q]\cdot FFT2(B[n, m]))) \tag{1} $$

其中 $B[n, m]$为输入图像， $m,n$为图像维数， $A[n, m]$ 为输出图像， $\angle$ 为角运算， $FFT2$ 为快速傅里叶变换，$IFFT2$ 为逆快速傅里叶变换，$p$和 $q$是二维频率变量，$\tilde{L}[p, q]$ 为局部频率响应核，通俗的讲，就是一个用于图像平滑、去噪的滤波核，论文中没有给出，可以使用一些用于图像平滑的滤波核代替， $\tilde{K}[p, q]$ 为相位核，其中，

$$ \tilde{K}[p, q]=e^{j\cdot\varphi[p,q]} $$

$$ \varphi[p,q]=\varphi_{polar}[r,\theta] \=\varphi_{polar}[r]\=S\cdot\frac{W\cdot r \cdot tan^{-1}(W \cdot r)-(1/2)\cdot ln(1+(W \cdot r)^2)}{W \cdot r_{max} \cdot tan^{-1}(W \cdot r_{max})-(1/2)ln(1+W \cdot r_{max})^2} \tag{2} $$

$r=\sqrt{p^2+q^2} $， $\theta=tan^{-1}(q/p)$ ，$W$ 是施加到图像相位的强度和扭曲，是影响图像分割效果的两个重要参数。

编程实践

PST算法中最核心的就是公式(1)，编程实现可以一步一步来实现公式中的每个模块。

首先导入需要的模块，

import os 
import numpy as np
import mahotas as mh
import matplotlib.pylab as plt
import cv2

定义全局变量，

L = 0.5 
S = 0.48 
W= 12.14
LPF=0.5
Threshold_min = -1
Threshold_max = 0.0019
FLAG = 1

计算公式中的核心参数， $r，\theta$ r，\theta ,

def cart2pol(x, y):
    theta = np.arctan2(y, x)
    rho = np.hypot(x, y)
    return theta, rho

生成变量 p 和 q ,

x = np.linspace(-L, L, img.shape[0])
y = np.linspace(-L, L, img.shape[1])
X, Y = np.meshgrid(x, y)
p, q = X.T, y.T
theta, rho = cart2pol(p, q)

接下来对公式(1)从右至左依次实现，

对输入图像进行快速傅里叶变换,

orig = np.fft.fft2(img)

实现 $\tilde{L}[p, q]$ \tilde{L}[p, q]，

expo = np.fft.fftshift(np.exp(-np.power((np.divide(rho, math.sqrt((LPF ** 2) / np.log(2)))), 2)))

对图像进行平滑处理，

orig_filtered = np.real(np.fft.ifft2((np.multiply(orig, expo))))

实现相位核，

PST_Kernel_1 = np.multiply(np.dot(rho, W), np.arctan(np.dot(rho, W))) - 0.5 * np.log(1 + np.power(np.dot(rho, W), 2))
PST_Kernel = PST_Kernel_1 / np.max(PST_Kernel_1) * S

将前面实现的部分与相位核做乘积，

temp = np.multiply(np.fft.fftshift(np.exp(-1j * PST_Kernel)), np.fft.fft2(orig_filtered))

对图像进行逆快速傅里叶变换，

temp = np.multiply(np.fft.fftshift(np.exp(-1j * PST_Kernel)), np.fft.fft2(Image_orig_filtered))
orig_filtered_PST = np.fft.ifft2(temp)

进行角运算，得到变换图像的相位，

PHI_features = np.angle(Image_orig_filtered_PST)

对图像进行阈值化处理，

features = np.zeros((PHI_features.shape[0], PHI_features.shape[1]))
features[PHI_features > Threshold_max] = 1 
features[PHI_features < Threshold_min] = 1  
features[I < (np.amax(I) / 20)] = 0

应用二进制形态学操作来清除转换后的图像,

out = features
out = mh.thin(out, 1)
out = mh.bwperim(out, 4)
out = mh.thin(out, 1)
out = mh.erode(out, np.ones((1, 1)))

到这里就完成了相位拉伸变换的核心部分，

def phase_stretch_transform(img, LPF, S, W, threshold_min, threshold_max, flag):
    L = 0.5
    x = np.linspace(-L, L, img.shape[0])
    y = np.linspace(-L, L, img.shape[1])
    [X1, Y1] = (np.meshgrid(x, y))
    X = X1.T
    Y = Y1.T
    theta, rho = cart2pol(X, Y)
    orig = ((np.fft.fft2(img)))
    expo = np.fft.fftshift(np.exp(-np.power((np.divide(rho, math.sqrt((LPF ** 2) / np.log(2)))), 2)))
    orig_filtered = np.real(np.fft.ifft2((np.multiply(orig, expo))))
    PST_Kernel_1 = np.multiply(np.dot(rho, W), np.arctan(np.dot(rho, W))) - 0.5 * np.log(
        1 + np.power(np.dot(rho, W), 2))
    PST_Kernel = PST_Kernel_1 / np.max(PST_Kernel_1) * S
    temp = np.multiply(np.fft.fftshift(np.exp(-1j * PST_Kernel)), np.fft.fft2(orig_filtered))
    orig_filtered_PST = np.fft.ifft2(temp)
    PHI_features = np.angle(orig_filtered_PST)
    if flag == 0:
        out = PHI_features
    else:
        features = np.zeros((PHI_features.shape[0], PHI_features.shape[1]))
        features[PHI_features > threshold_max] = 1
        features[PHI_features < threshold_min] = 1
        features[img < (np.amax(img) / 20)] = 0

        out = features
        out = mh.thin(out, 1)
        out = mh.bwperim(out, 4)
        out = mh.thin(out, 1)
        out = mh.erode(out, np.ones((1, 1)))
    return out, PST_Kernel

下面完成调用部分的功能，

首先读取函数并把图像转化为灰度图，

Image_orig = mh.imread("./cameraman.tif")
if Image_orig.ndim == 3:
    Image_orig_grey = mh.colors.rgb2grey(Image_orig) 
else: 
    Image_orig_grey = Image_orig

调用前面的函数，对图像进行相位拉伸变换，

edge, kernel = phase_stretch_transform(Image_orig_grey, LPF, Phase_strength, Warp_strength, Threshold_min, Threshold_max, Morph_flag)

显示图像，

Overlay = mh.overlay(Image_orig_grey, edge)
edge = edge.astype(np.uint8)*255
plt.imshow(Edge)
plt.show()

主函数的完整内容为，

def main():
    Image_orig = mh.imread("./cameraman.tif")
    if Image_orig.ndim == 3:
       Image_orig_grey = mh.colors.rgb2grey(Image_orig)
    else:
       Image_orig_grey = Image_orig
    edge, kernel = phase_stretch_transform(Image_orig_grey, LPF, S, W, Threshold_min,
                                           Threshold_max, FLAG)
    Overlay = mh.overlay(Image_orig_grey, edge)
    Edge = edge.astype(np.uint8)*255
    plt.imshow(Edge)
    plt.show()

1.4 图像预处理之图像增广

前言

近几年深度学习的大规模成功应用主要的就是得益于数据的累积和算例的提升，虽然近几年很多研究者竭力的攻克半监督和无监督学习，减少对大量数据的依赖，但是目前数据在计算机视觉、自然语言处理等人工智能技术领域依然占据着非常重要的地位。甚至可以说，大规模的数据是计算机视觉成功应用的前提条件。但是由于种种原因导致数据的采集变的十分困难，因此图像增广技术就在数据的准备过程中占据着举足轻重的角色，本文就概括一下常用的图像增广技术并编程实现相应手段。

介绍

图像增广（image augmentation）技术通过对训练图像做一系列随机改变，来产生相似但又不同的训练样本，从而扩大训练数据集的规模。图像增广的另一种解释是，随机改变训练样本可以降低模型对某些属性的依赖，从而提高模型的泛化能力。

目前常用的图像增广技术有如下几种：

镜像变换
旋转
缩放
裁剪
平移
亮度修改
添加噪声
剪切
变换颜色

在图像增广过程中可以使用其中一种手段进行扩充，也可以使用其中的几种方法进行组合使用，由于概念比较简单，容易理解，所以接下来就边实现，边详细阐述理论知识。

几何变换

首先以水平镜像为例，假设在原图中像素的坐标为，在镜像变换之后的图像中的坐标为，原图像坐标和镜像变换后的坐标之间的关系式： $$ \left{ \begin{aligned} x_1 &=& w-1-x_0 \ y_1 &=& y_0 \end{aligned} \right. $$

其中 w 为图像的宽度。

那么两张图像的关系就是： $$ \left[ \begin{array}{c}{x_{1}} \ {y_{1}} \ {1}\end{array}\right]=\left[ \begin{array}{ccc}{-1} & {0} & {w-1} \ {0} & {1} & {0} \ {0} & {0} & {1}\end{array}\right] \left[ \begin{array}{l}{x_{0}} \ {y_{0}} \ {1}\end{array}\right] $$

它的逆变换就是 $$ \left[ \begin{array}{c}{x_{0}} \ {y_{0}} \ {1}\end{array}\right]=\left[ \begin{array}{ccc}{-1} & {0} & {w-1} \ {0} & {1} & {0} \ {0} & {0} & {1}\end{array}\right] \left[ \begin{array}{l}{x_{1}} \ {y_{1}} \ {1}\end{array}\right] $$

从原图到水平镜像的变换矩阵就是： $$ \left[ \begin{array}{ccc}{-1} & {0} & {w-1} \ {0} & {1} & {0} \ {0} & {0} & {1}\end{array}\right] $$

同理，可知，垂直镜像变换的关系式为： $$ \left[ \begin{array}{ccc}{-1} & {0} & {w-1} \ {0} & {1} & {0} \ {0} & {0} & {1}\end{array}\right] $$

其中为图像高度。

通过上述可以知道，平移变换的数学矩阵为： $$ H=\left[ \begin{array}{lll}{1} & {0} & {d_{x}} \ {0} & {1} & {d_{y}} \ {0} & {0} & {1}\end{array}\right] $$

其中和分别是像素在水平和垂直方向移动的距离。

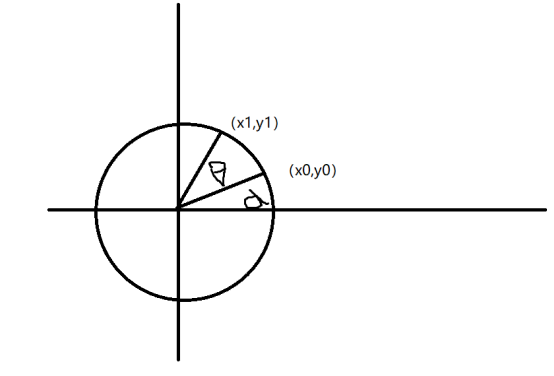
同理可以推广到旋转变换上，加上原像素的坐标为 $(x_0,y_0) $，该像素点相对于原点的角度为，假设有一个半径为的圆，那么原像素的坐标可以表示为： $$ \left{\begin{array}{l}{x_{0}=r \cos \alpha} \ {y_{0}=r \cos \alpha}\end{array}\right. $$

加上旋转后的像素坐标为 $(x_1,y_1)$，旋转角度为$\theta$那么可以表示为： $$ \left{\begin{array}{l}{x_1=r \cos (\alpha+\theta)} \ {y_1=r \sin (\alpha+\theta)}\end{array}\right. $$

通过展开、化简可得， $$ \left{\begin{array}{l}{x_1=r \cos (\alpha+\theta)=r \cos \alpha \cos \theta-r \sin \alpha \sin \theta=x_{0} \cos \theta-y_{0} \sin \theta} \ {y_1=r \sin (\alpha+\theta)=r \sin \alpha \cos \theta+r \cos \alpha \sin \theta=x_{0} \sin \theta+y_{0} \cos \theta}\end{array}\right. $$

把上述公式写成数学矩阵形式为： $$ \left[ \begin{array}{l}{x_1} \ {y_1} \ {1}\end{array}\right]=\left[ \begin{array}{ccc}{\cos \theta} & {-\sin \theta} & {0} \ {\sin \theta} & {\cos \theta} & {0} \ {0} & {0} & {1}\end{array}\right] \left[ \begin{array}{l}{x_{0}} \ {y_{0}} \ {1}\end{array}\right] $$

因此旋转变换的矩阵为： $$ H=\left[ \begin{array}{ccc}{\cos \theta} & {-\sin \theta} & {0} \ {\sin \theta} & {\cos \theta} & {0} \ {0} & {0} & {1}\end{array}\right] $$

其他的几何变换方式和上述提到的核心思想大同小异，因此，就不再详细展开，感兴趣的可以在网上搜集一下，或者看一下数字图像处理相关的书籍，关注这些内容的讲解有很多。

编程实践

编程实践过程中主要用到opencv、numpy和skimage。

读取图像：

# 1. 读取图像
img = cv2.imread("./data/000023.jpg")
cv2.imshow("Origin", img)
cv2.waitKey()

初始化一个矩阵，用于存储转化后的图像，

generate_img = np.zeros(img.shape)

1.水平镜像

遍历图像的像素，用前文提到的数学关系式进行像素的转化，

for i in range(h):
    for j in range(w):
        generate_img[i, w - 1 - j] = img[i, j]

cv2.imshow("Ver", generate_img.astype(np.uint8))
cv2.waitKey()

备注：初始化的图像数据类型是numpy.float64，用opencv显示时无法正常显示，因此在显示时需要用astype(np.uint8)把图像转化成numpy.uint8数据格式。

2.垂直镜像

垂直镜像变换代码，

for i in range(h):
    for j in range(w):
        generate_img[h-1-i, j] = img[i, j]

镜像变换也可以直接调用opencv的flip进行使用。

3.图像缩放

这个比较简单，直接调用opencv的resize函数即可，

output = cv2.resize(img, (100, 300))

4.旋转变换

这个相对复杂一些，需要首先用getRotationMatrix2D函数获取一个旋转矩阵，然后调用opencv的warpAffine仿射函数安装旋转矩阵对图像进行旋转变换，

center = cv2.getRotationMatrix2D((w/2, h/2), 45, 1)
rotated_img = cv2.warpAffine(img, center, (w, h))

5. 平移变换

首先用numpy生成一个平移矩阵，然后用仿射变换函数对图像进行平移变换，

move = np.float32([[1, 0, 100], [0, 1, 100]])
move_img = cv2.warpAffine(img, move, (w, h))

6.亮度变换

亮度变换的方法有很多种，本文介绍一种叠加图像的方式，通过给原图像叠加一副同样大小，不同透明度的全零像素图像来修改图像的亮度，

alpha = 1.5
light = cv2.addWeighted(img, alpha, np.zeros(img.shape).astype(np.uint8), 1-alpha, 3)

其中alpha是原图像的透明度，

7.添加噪声

首先写一下噪声添加的函数，原理就是给图像添加一些符合正态分布的随机数，

def add_noise(img):
    img = np.multiply(img, 1. / 255,
                        dtype=np.float64)
    mean, var = 0, 0.01
    noise = np.random.normal(mean, var ** 0.5,
                             img.shape)
    img = convert(img, np.floating)
    out = img + noise
    return out

8.组合变换

除了以上方法单独使用之外，还可以叠加其中多种方法进行组合使用，比如可以结合选择、镜像进行使用，

完整代码如下：

import cv2
import numpy as np
from skimage.util.dtype import convert


class ImageAugmented(object):
    def __init__(self, path="./data/000023.jpg"):
        self.img = cv2.imread(path)
        self.h, self.w = self.img.shape[0], self.img.shape[1]
    
    # 1. 镜像变换
    def flip(self, flag="h"):
        generate_img = np.zeros(self.img.shape)
        if flag == "h":
            for i in range(self.h):
                for j in range(self.w):
                    generate_img[i, self.h - 1 - j] = self.img[i, j]
        else:
            for i in range(self.h):
                for j in range(self.w):
                    generate_img[self.h-1-i, j] = self.img[i, j]
        return generate_img

    # 2. 缩放
    def _resize_img(self, shape=(100, 300)):
        return cv2.resize(self.img, shape)
    
    # 3. 旋转
    def rotated(self):
        center = cv2.getRotationMatrix2D((self.w / 2, self.h / 2), 45,1)
        return cv2.warpAffine(self.img, center, (self.w, self.h))
    
    # 4. 平移
    def translation(self, x_scale=100, y_scale=100):
        move = np.float32([[1, 0, x_scale], [0, 1, y_scale]])
        return cv2.warpAffine(self.img, move, (self.w, self.h))
    
    # 5. 改变亮度
    def change_light(self, alpha=1.5, scale=3):
        return cv2.addWeighted(self.img, alpha, np.zeros(self.img.shape).astype(np.uint8), 1-alpha, scale)
    
    # 6. 添加噪声
    def add_noise(self, mean=0, var=0.01):
        img = np.multiply(self.img, 1. / 255, dtype=np.float64)
        noise = np.random.normal(mean, var ** 0.5,
                                 img.shape)
        img = convert(img, np.floating)
        out = img + noise
        return out

第二章传统目标检测

2.1 特征工程

前言

随着2012年AlexNet在ImageNet挑战赛一举夺魁，让深度卷积网络迅速霸占了目标识别和计算机视觉的头把交椅。随后的VGG、R-CNN、SSD、YOLO让深度卷积网络在计算机视觉领域的地位更加稳固。

由于深度卷积网络在目标识别方面表现得太过于抢眼，所以，很多入门计算机视觉的同学会选择从深度学习切入，目前惯用的学习套路莫过于如下几条：

吴恩达《机器学习》《深度学习工程师》
李飞飞《cs231n》
clone开源代码
微调代码跑模型
......

整个过程中很少涉及图像底层的内容，甚至知名的cs231课程对传统目标识别也未丝毫提及。

对于这个问题不难理解，深度学习与传统目标识别有着最根本的区别。

传统目标识别有两个非常重要的步骤：特征提取和机器学习。尤其是特征提取需要人为选取特征和特征后处理，特征的好坏对于识别的精确度有着至关重要的作用。而深度学习只需要对数据进行预处理输入到卷积神经网络中，特征提取由卷积神经网络自行完成，不需要人为干预特征的选取。

避免了人为特征提取的确给目标识别带来了质的飞跃，但是我认为计算机视觉依然脱离不了图像的范畴，它依然是一门以图像为根本的技术。目前深度计算机视觉模型的可迁移性差也体现出这一点，不能忽略不同类型图像之间的差异性。

例如，

自然图像
遥感图像
医学图像

三者之间有着巨大的差异性，在进行模型的学习过程中需要充分考虑不同类型图像的特点，这样对于模型的学习也有着非常大的益处。

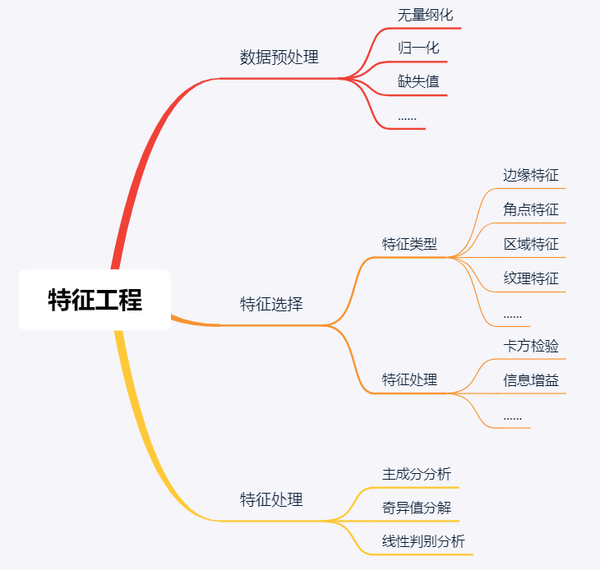
特征工程

特征工程在传统目标识别中占据着举足轻重的地位，甚至可以说，特征工程做的好坏能够直接影响最终识别的精度。

特征工程主要包括三个部分：

数据预处理
特征提取
特征后处理

数据预处理主要用一些手段和技术对数据做一下处理：

无量纲化
缺失值
归一化
标准化
......

这项工作基础而且重要，数据的准确性是识别效果的前提条件。

特征后处理主要包括如下几项：

主成分分析
奇异值分解
线性判别分析

目前常用的特征后处理手段就是对特征进行降维，由特征降维主要有如下几项优点：

降低计算开销
获取有价值的信息
去除噪声
使得数据更加易用
......

关于图像预处理的内容前面已经用几讲进行阐述，这里就不再阐述。关于特征降维的知识后续会详细介绍，本阶段主要围绕特征提取进行讲解。

特征提取

特征提取主要的目的是在图像中提取出一些有价值的信息，在传统目标识别中所占地位丝毫不亚于支持向量机、Adaboost这类机器学习算法。在特征选择的过程中需要充分考虑目标的相关性，这样才能提取更加能够描述目标类别的特征，进而影响到目标检测的精度。

目前的特征种类有非常多，颜色特征、纹理特征、区域特征、边缘特征等，本文不过多介绍这类概念性的内容，主要概括一些常用的特征描述子，后续文章会逐个对这些经典的特征提取算法进行展开和详解。

传统目标识别中常用的特征描述子有：

Harris
SIFT
SURF
LBP
HOG
DPM

Harris是一种角点特征描述子，角点对应于物体的拐角，道路的十字路口、丁字路口等，在现实中非常常见，因此，Harris一直以来都是一个非常热门的特征检测算法。

Harris角点特征

SIFT，即尺度不变特征变换（Scale-invariant feature transform，SIFT），该方法于1999年由David Lowe发表在ICCV。由于该算法对旋转、尺度缩放、亮度变化保持不变性，对视角变化、仿射变换、噪声也保持一定程度的稳定性，使其备受关注，

SIFT提取特征点

SIFT有着非常多的优点，但是也有一点致命的缺陷--实时性不足。SURF（Speeded Up Robust Features）改进了特征的提取和描述方式，用一种更为高效的方式完成特征的提取和描述。

SURF提取特征点

方向梯度直方图（Histogram of Oriented Gradient, HOG）特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子，这个名气就更大了。它是一种基于统计的特征提取算法，通过统计不同梯度方向的像素而获取图像的特征向量。

HOG特征

LBP（Local Binary Pattern，局部二值模式），它是首先由T. Ojala, M.Pietikäinen,和 D. Harwood 在1994年提出，是一种纹理特征描述算子，旋转不变性和灰度不变性等显著的优点。

LBP特征

DPM(Discriminatively Trained Part Based Models)是Felzenszwalb力作，作者在这个算法中提出了很多对后续目标识别甚至深度学习影响深远的思想，作者也因此一举获得VOC挑战赛的终身成就奖。

DPM算法

由于时间问题，本文仅仅是概括性的介绍一下传统目标检测中常用的特征描述子，后续会单独对每个算法详细展开并一步一步编程实践。

2.2 Harris角点检测

前言

在传统目标识别中，特征提取是最终目标识别效果好坏的一个重要决定因素，因此，在这项工作里，有很多研究者把主要精力都放在特征提取方向。在传统目标识别中，主要使用的特征主要有如下几类：

边缘特征
纹理特征
区域特征
角点特征

本文要讲述的Harris角点检测就是焦点特征的一种。

目前角点检测算法主要可归纳为3类：

基于灰度图像的角点检测
基于二值图像的角点检测
基于轮廓的角点检测

因为角点在现实生活场景中非常常见，因此，角点检测算法也是一种非常受欢迎的检测算法，尤其本文要讲的Harris角点检测，可以说传统检测算法中的经典之作。

什么是角点？

要想弄明白角点检测，首先要明确一个问题，什么是角点？

这个在现实中非常常见，例如图中标记出的飞机的角点，除此之外例如桌角、房角等。这样很容易理解，但是该怎么用书面的语言阐述角点？

角点就是轮廓之间的交点。

如果从数字图像处理的角度来描述就是：像素点附近区域像素无论是在梯度方向、还是在梯度幅值上都发生较大的变化。

这句话是焦点检测的关键，也是精髓，角点检测算法的思想就是由此而延伸出来的。

角点检测的算法思想是：选取一个固定的窗口在图像上以任意方向的滑动，如果灰度都有较大的变化，那么久认为这个窗口内部存在角点。

要想实现角点检测，需要用数学语言对其进行描述，下面就着重用数学语言描述一下角点检测算法的流程和原理。

用 $w(x,y)$ 表示窗口函数，$[u,v]$ 为窗口平移量，像素在窗口内的变化量为，

$$ E(u, v)=\sum_{x, y} w(x, y)[I(x+u, y+v)-I(x, y)]^{2} $$

其中 $I(x, y)$ 为平移前的像素灰度值， $I(x+u, y+v)$为平移后的像素灰度值，

通过对灰度变化部分进行泰勒展开。

因此得到，

$$ E(u, v) \cong[u, v] M \left[ \begin{array}{l}{u} \ {v}\end{array}\right] $$

矩阵 $M$中 $I_x$、 $I_y$分别是像素在 $x$ 、 $y$ 方向的梯度，从上述化简公式可以看出，灰度变化的大小主要取决于矩阵，

$$ M=\sum_{x, y} W(x, y) \left[ \begin{array}{cc}{I_{x}(x, y)^{2}} & {I_{x}(x, y) I_{y}(x, y)} \ {I_{x}(x, y) I_{y}(x, y)} & {I_{y}(x, y)^{2}}\end{array}\right] $$

现在在回过头来看一下角点与其他类型区域的不同之处：

平坦区域：梯度方向各异，但是梯度幅值变化不大
线性边缘：梯度幅值改变较大，梯度方向改变不大
角点：梯度方向和梯度幅值变化都较大

明白上述3点之后看一下怎么利用其矩阵 M 进行角点检测。

根据主成分分析(PCA)的原理可知，如果对矩阵 M 对角化，那么，特征值就是主分量上的方差，矩阵是二维的方阵，有两个主分量，如果在窗口区域内是角点，那么梯度变化会较大，像素点的梯度分布比较离散，这体现在特征值上就是特征值比较大。

换句话说，

如果矩阵对应的两个特征值都较大，那么窗口内含有角点
如果特征值一个大一个小，那么窗口内含有线性边缘
如果两个特征值都很小，那么窗口内为平坦区域

读到这里就应该明白了，角点的检测转化为数学模型，就是求解窗口内矩阵的特征值并且判断特征值的大小。

如果要评价角点的强度，可以用下方公式，

$$ R=\operatorname{det} M-k(\operatorname{trace} M)^{2} \tag{1} $$

其中，

$$ \operatorname{det} M=\lambda_{1} \lambda_{2} $$

$$ \operatorname{trace} M=\lambda_{1}+\lambda_{2} $$

编程实践

因为Harris角点检测算法非常经典，因此，一些成熟的图像处理或视觉库都会直接提供Harris角点检测的算法，以OpenCV为例，

import cv2
import numpy as np

filename = '2007_000480.jpg'

img = cv2.imread(filename)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
gray = np.float32(gray)
dst = cv2.cornerHarris(gray,blockSize,ksize,k)

"""
其中，
gray为灰度图像，
blockSize为邻域窗口的大小，
ksize是用于Soble算子的参数，
k是一个常量，取值为0.04~0.06
"""

因为本文要讲一步一步实现Harris角点检测算法，因此，对OpenCV提供的函数不多阐述，下面开始一步一步实现Harris角点检测算法。

检点检测算法的流程如下：

利用公式(1)求出输入图像每个位置的角点强度响应
给定阈值，当一个位置的强度大于阈值则认为是角点
画出角点

首先是第一步，根据上述提到的公式求矩阵的特征值和矩阵的迹，然后计算图像的角点强度，这里选取常数k=0.04，

def calculate_corner_strength(img, scale=3, k=0.06):
    # 计算图像在x、y方向的梯度
    # 用滤波器采用差分求梯度的方式
    gradient_imx, gradient_imy = zeros(img.shape), zeros(img.shape)
    filters.gaussian_filter(img, (scale, scale), (0, 1), gradient_imx)
    filters.gaussian_filter(img, (scale, scale), (1, 0), gradient_imy)

    # 计算矩阵M的每个分量
    I_xx = filters.gaussian_filter(gradient_imx*gradient_imx, scale)
    I_xy = filters.gaussian_filter(gradient_imx*gradient_imy, scale)
    I_yy = filters.gaussian_filter(gradient_imy*gradient_imy, scale)

    # 计算矩阵的迹、特征值和响应强度
    det_M = I_xx * I_yy - I_xy ** 2
    trace_M = I_xx + I_yy
    return det_M + k * trace_M ** 2

接下来完成第2步，根据给定阈值，获取角点，

def corner_detect(img, min=15, threshold=0.04):
    # 首先对图像进行阈值处理
    _threshold = img.max() * threshold
    threshold_img = (img > _threshold) * 1
    coords = array(threshold_img.nonzero()).T
    candidate_values = [img[c[0], c[1]] for c in coords]
    index = argsort(candidate_values)

    # 选取领域空间，如果邻域空间距离小于min的则只选取一个角点
    # 防止角点过于密集
    neighbor = zeros(img.shape)
    neighbor[min:-min, min:-min] = 1
    filtered_coords = []
    for i in index:
        if neighbor[coords[i, 0], coords[i, 1]] == 1:
            filtered_coords.append(coords[i])
            neighbor[(coords[i, 0] - min):(coords[i, 0] + min),
            (coords[i, 1] - min):(coords[i, 1] + min)] = 0
    return filtered_coords

然后是画出角点，

def corner_plot(image, filtered_coords):
    figure()
    gray()
    imshow(image)
    plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], 'ro')
    axis('off')
    show()

检测结果，

完整代码如下，

from scipy.ndimage import filters
import cv2
from matplotlib.pylab import *


class Harris(object):
    def __init__(self, img_path):
        self.img = cv2.imread(img_path, 0)

    def calculate_corner_strength(self):
        # 计算图像在x、y方向的梯度
        # 用滤波器采用差分求梯度的方式
        scale = self.scale
        k = self.k
        img = self.img
        gradient_imx, gradient_imy = zeros(img.shape), zeros(img.shape)
        filters.gaussian_filter(img, (scale, scale), (0, 1), gradient_imx)
        filters.gaussian_filter(img, (scale, scale), (1, 0), gradient_imy)

        # 计算矩阵M的每个分量
        I_xx = filters.gaussian_filter(gradient_imx*gradient_imx, scale)
        I_xy = filters.gaussian_filter(gradient_imx*gradient_imy, scale)
        I_yy = filters.gaussian_filter(gradient_imy*gradient_imy, scale)

        # 计算矩阵的迹、特征值和响应强度
        det_M = I_xx * I_yy - I_xy ** 2
        trace_M = I_xx + I_yy
        return det_M + k * trace_M ** 2

    def corner_detect(self, img):
        # 首先对图像进行阈值处理
        _threshold = img.max() * self.threshold
        threshold_img = (img > _threshold) * 1
        coords = array(threshold_img.nonzero()).T
        candidate_values = [img[c[0], c[1]] for c in coords]
        index = argsort(candidate_values)

        # 选取领域空间，如果邻域空间距离小于min的则只选取一个角点
        # 防止角点过于密集
        neighbor = zeros(img.shape)
        neighbor[self.min:-self.min, self.min:-self.min] = 1
        filtered_coords = []
        for i in index:
            if neighbor[coords[i, 0], coords[i, 1]] == 1:
                filtered_coords.append(coords[i])
                neighbor[(coords[i, 0] - self.min):(coords[i, 0] + self.min),
                (coords[i, 1] - self.min):(coords[i, 1] + self.min)] = 0
        return filtered_coords

    def corner_plot(self, img, corner_img):
        figure()
        gray()
        imshow(img)
        plot([p[1] for p in corner_img], [p[0] for p in corner_img], 'ro')
        axis('off')
        show()

    def __call__(self, k=0.04, scale=3, min=15, threshold=0.03):
        self.k = k
        self.scale = scale
        self.min = min
        self.threshold = threshold
        strength_img = self.calculate_corner_strength()
        corner_img = self.corner_detect(strength_img)
        self.corner_plot(self.img, corner_img)


if __name__ == '__main__':
    harris = Harris("2007_002619.jpg")
    harris()

2.3 SIFT特征

前言

提到传统目标识别，就不得不提SIFT算法，Scale-invariant feature transform，中文含义就是尺度不变特征变换。此方法由David Lowe于1999年发表于ICCV(International Conference on Computer Vision)，并经过5年的整理和晚上，在2004年发表于IJCV(International journal of computer vision)。由于在此之前的目标检测算法对图片的大小、旋转非常敏感，而SIFT算法是一种基于局部兴趣点的算法，因此不仅对图片大小和旋转不敏感，而且对光照、噪声等影响的抗击能力也非常优秀，因此，该算法在性能和适用范围方面较于之前的算法有着质的改变。这使得该算法对比于之前的算法有着明显的优势，所以，一直以来它都在目标检测和特征提取方向占据着重要的地位，截止2019年6月19日，这篇文章的引用量已经达到51330次(谷歌学术)，受欢迎程度可见一斑，本文就详细介绍一下这篇文章的原理，并一步一步编程实现本算法，让各位对这个算法有更清晰的认识和理解。

SIFT

前面提到，SIFT是一个非常经典而且受欢迎的特征描述算法，因此关于这篇文章的学习资料、文章介绍自然非常多。但是很多文章都相当于把原文翻译一遍，花大量篇幅在讲高斯模糊、尺度空间理论、高斯金字塔等内容，容易让人云里雾里，不知道这种算法到底在讲什么？重点又在哪里？

图1 SIFT算法步骤

其实下载这篇文章之后打开看一下会发现，SIFT的思想并没有想的那么复杂，它主要包含4个步骤：

尺度空间极值检测：通过使用高斯差分函数来计算并搜索所有尺度上的图像位置，用于识别对尺度和方向不变的潜在兴趣点。

关键点定位：通过一个拟合精细的模型在每个候选位置上确定位置和尺度，关键点的选择依赖于它们的稳定程度。

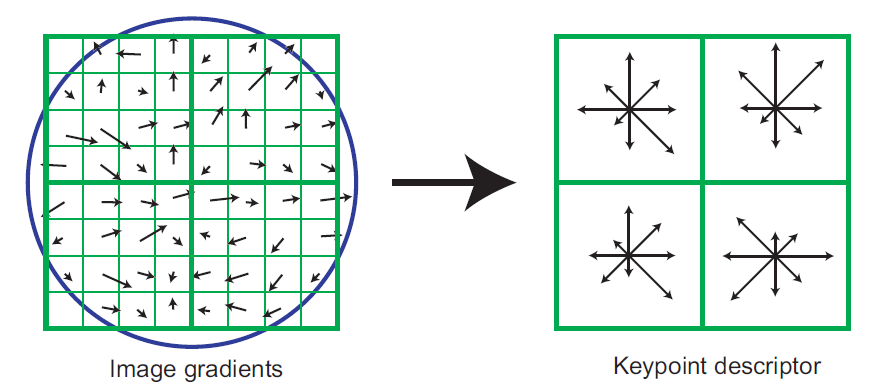
方向匹配：基于局部图像的梯度方向，为每个关键点位置分配一个或多个方向，后续所有对图像数据的操作都是相对于关键点的方向、尺度和位置进行变换，从而而这些变换提供了不变形。
关键点描述：这个和HOG算法有点类似之处，在每个关键点周围的区域内以选定的比例计算局部图像梯度，这些梯度被变换成一种表示，这种表示允许比较大的局部形状的变形和光照变化。

由于它将图像数据转换为相对于局部特征的尺度不变坐标，因此这种方法被称为尺度不变特征变换。

如果对这个算法思路进行简化，它就包括2个部分：

特征提取
特征描述

特征提取

特征点检测主要分为如下两个部分，

候选关键点
关键点定位

候选关键点

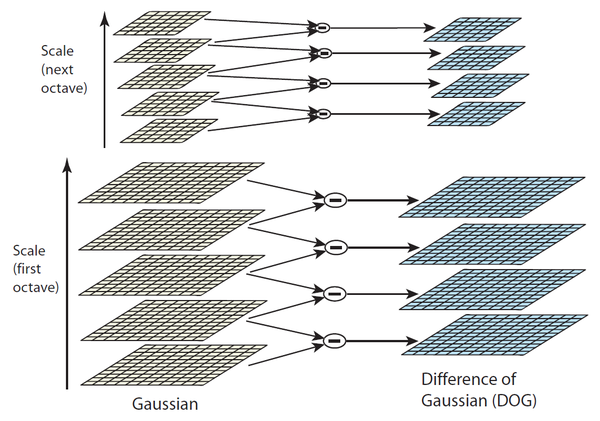
Koenderink（1984）和Lindeberg（1994）已经证明，在各种合理的假设下，高斯函数是唯一可能的尺度空间核。因此，图像的尺度空间被定义为函数，它是由一个可变尺度的高斯核和输入图像生成，其中高斯核为，为了有效检测尺度空间中稳定的极点，Lowe于1999年提出在高斯差分函数(DOG)中使用尺度空间极值与图像做卷积，这可以通过由常数乘法因子分隔的两个相邻尺度的差来计算。用公式表示就是，由于平滑区域临近像素之间变化不大，但是在边、角、点这些特征较丰富的地方变化较大，因此通过DOG比较临近像素可以检测出候选关键点。

关键点定位

检测出候选关键点之后，下一步就是通过拟合惊喜的模型来确定位置和尺度。 2002年Brown提出了一种用3D二次函数来你和局部样本点，来确定最大值的插值位置，实验表明，这使得匹配和稳定性得到了实质的改进。他的具体方法是对函数进行泰勒展开，上述的展开式，就是所要的拟合函数。极值点的偏移量为，如果偏移量在任何一个维度上大于0.5时，则认为插值中心已经偏移到它的邻近点上，所以需要改变当前关键点的位置，同时在新的位置上重复采用插值直到收敛为止。如果超出预先设定的迭代次数或者超出图像的边界，则删除这个点。

特征描述

前面讲了一些有关特征点检测的内容，但是SIFT实质的内容和价值并不在于特征点的检测，而是特征描述思想，这是它的核心所在，特征点描述主要包括如下两点：

方向分配
局部特征描述

方向分配

根据图像的图像，可以为每个关键定指定一个基准方向，可以相对于这个指定方向表示关键点的描述符，从而实现了图像的旋转不变性。关键点的尺度用于选择尺度最接近的高斯平滑图像，使得计算是以尺度不变的方式执行，对每个图像，分别计算它的梯度幅值和梯度方向，然后，使用方向直方图统计关键点邻域内的梯度幅值和梯度方向。将0~360度划分成36个区间，每个区间为10度，统计得出的直方图峰值代表关键点的主方向。

局部特征描述

通过前面的一系列操作，已经获得每个关键点的位置、尺度、方向，接下来要做的就是用已知特征向量把它描述出来，这是图像特征提取的核心部分。为了避免对光照、视角等因素的敏感性，需要特征描述子不仅仅包含关键点，还要包含它的邻域信息。

SIFT使用的特征描述子和后面要讲的HOG有很多相似之处。它一检测得到的关键点为中心，选择一个1616的邻域，然后再把这个邻域再划分为44的子区域，然后对梯度方向进行划分成8个区间，这样在每个子区域内疚会得到一个448=128维的特征向量，向量元素大小为每个梯度方向区间权值。提出得到特征向量后要对邻域的特征向量进行归一化，归一化的方向是计算邻域关键点的主方向，并将邻域旋转至根据主方向旋转至特定方向，这样就使得特征具有旋转不变性。然后再根据邻域内各像素的大小把邻域缩放到指定尺度，进一步使得特征描述子具有尺度不变性。

以上就是SIFT算法的核心部分。

编程实践

本文代码已经放在github，感兴趣的可以自行查看，

https://github.com/jakpopc/aiLearnNotes/blob/master/computer_vision/SIFT.pygithub.com

本文实现SIFT特征检测主要基于以下工具包：

OpenCV
numpy

其中OpenCV是一个非常知名且受欢迎的跨平台计算机视觉库，它不仅包含常用的图像读取、显示、颜色变换，还包含一些为人熟知的经典特征检测算法，其中就包括SIFT，所以本文使用OpenCV进行读取和SIFT特征检测。 numpy是一个非常优秀的数值计算库，也常用于图像的处理，这里使用numpy主要用于图像的拼接和显示。

导入工具包

import numpy as np
import cv2

图像准备

首先写一下读取图像的函数，

def load_image(path, gray=True):
    if gray:
        img = cv2.imread(path)
        return cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
    else:
        return cv2.imread(path)

然后，生成一副对原图进行变换的图像，用于后面特征匹配，本文选择对图像进行垂直镜像变换，

def transform(origin):
    h, w = origin.shape
    generate_img = np.zeros(origin.shape)
    for i in range(h):
        for j in range(w):
            generate_img[i, w - 1 - j] = origin[i, j]
    return generate_img.astype(np.uint8)

显示一下图像变换的结果，

img1 = load_image('2007_002545.jpg')
img2 = transform(img1)
combine = np.hstack((img1, img2))
cv2.imshow("gray", combine)
cv2.waitKey(0)

先用 xfeatures2d 模块实例化一个sift算子，然后使用 detectAndCompute 计算关键点和描述子，随后再用 drawKeypoints 绘出关键点，

# 实例化
sift = cv2.xfeatures2d.SIFT_create()

# 计算关键点和描述子
# 其中kp为关键点keypoints
# des为描述子descriptors
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)

# 绘出关键点
# 其中参数分别是源图像、关键点、输出图像、显示颜色
img3 = cv2.drawKeypoints(img1, kp1, img1, color=(0, 255, 255))
img4 = cv2.drawKeypoints(img2, kp2, img2, color=(0, 255, 255))

显示出检测的关键点为，

关键点已经检测出来，最后一步要做的就是绘出匹配效果，本文用到的是利用 FlannBasedMatcher 来显示匹配效果，首先要对 FlannBasedMatcher 进行参数设计和实例化，然后用 *knn 对前面计算的出的特征描述子进行匹配，最后利用 drawMatchesKnn 显示匹配效果，

# 参数设计和实例化
index_params = dict(algorithm=1, trees=6)
search_params = dict(checks=50)
flann = cv2.FlannBasedMatcher(index_params, search_params)

# 利用knn计算两个描述子的匹配
matche = flann.knnMatch(des1, des2, k=2)
matchesMask = [[0, 0] for i in range(len(matche))]

# 绘出匹配效果
result = []
for m, n in matche:
    if m.distance < 0.6 * n.distance:
        result.append([m])

img5 = cv2.drawMatchesKnn(img1, kp1, img2, kp2, matche, None, flags=2)
cv2.imshow("MatchResult", img5)
cv2.waitKey(0)

检测结果，

完整代码如下，

import numpy as np
import cv2


def load_image(path, gray=False):
    if gray:
        img = cv2.imread(path)
        return cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
    else:
        return cv2.imread(path)


def transform(origin):
    h, w, _ = origin.shape
    generate_img = np.zeros(origin.shape)
    for i in range(h):
        for j in range(w):
            generate_img[i, w - 1 - j] = origin[i, j]
    return generate_img.astype(np.uint8)


def main():
    img1 = load_image('2007_002545.jpg')
    img2 = transform(img1)

    # 实例化
    sift = cv2.xfeatures2d.SIFT_create()

    # 计算关键点和描述子
    # 其中kp为关键点keypoints
    # des为描述子descriptors
    kp1, des1 = sift.detectAndCompute(img1, None)
    kp2, des2 = sift.detectAndCompute(img2, None)

    # 绘出关键点
    # 其中参数分别是源图像、关键点、输出图像、显示颜色
    img3 = cv2.drawKeypoints(img1, kp1, img1, color=(0, 255, 255))
    img4 = cv2.drawKeypoints(img2, kp2, img2, color=(0, 255, 255))

    # 参数设计和实例化
    index_params = dict(algorithm=1, trees=6)
    search_params = dict(checks=50)
    flann = cv2.FlannBasedMatcher(index_params, search_params)

    # 利用knn计算两个描述子的匹配
    matche = flann.knnMatch(des1, des2, k=2)
    matchesMask = [[0, 0] for i in range(len(matche))]

    # 绘出匹配效果
    result = []
    for m, n in matche:
        if m.distance < 0.6 * n.distance:
            result.append([m])

    img5 = cv2.drawMatchesKnn(img1, kp1, img2, kp2, matche, None, flags=2)
    cv2.imshow("MatchResult", img5)
    cv2.waitKey(0)


if __name__ == '__main__':
    main()

以上就是SIFT的完整内容。

2.4 HOG特征

前言

如果自称为计算机视觉工程师，没有听说过前文提到的尺度不变特征变换(SIFT)，可以理解，但是如果没有听说过方向梯度直方图(Histogram of oriented gradient，HOG)，就有一些令人诧异了。这项技术是有发过国家计算机技术和控制研究所(INRIA)的两位研究院Navneet Dalal和Bill Triggs在2005年CVPR上首先发表提出(那时的CVPR含金量还是很高的)。原文Histograms of oriented gradients for human detection截止2019年7月10日引用率已经达到26856。

HOG通过计算局部图像提取的方向信息统计值来统计图像的梯度特征，它跟EOH、SIFT及shape contexts有诸多相似之处，但是它有明显的不同之处：HOG特征描述子是在一个网格秘籍、大小统一的细胞单元上进行计算，而且为了提高性能，它还采用了局部对比度归一化思想。它的出现，使得目标检测技术在静态图像的人物检测、车辆检测等方向得到大量应用。

在传统目标检测中，HOG可以称得上是经典中的经典，它的HOG+SVM+归一化思想对后面的研究产生深远的影响，包括后面要讲到的神作DPM，可以说，HOG的出现，奠定了2005之后的传统目标检测的基调和方向，下面就来了解一下这个经典之作。

方向梯度直方图

HOG特征的算法可以用一下几个部分概括，

梯度计算
单元划分
区块选择
区间归一化
SVM分类器

下面分别来详细阐述一下。

梯度计算

由于后面要进行归一化处理，因此在HOG中不需要像其他算法那样需要进行预处理，因此，第一步就成了梯度计算。为什么选择梯度特征？因为在目标边缘处灰度变化较大，因此，在边缘处灰度的梯度就较为明显，所以，梯度能够更好的表征目标的特征。

我们都知道在数学中计算梯度需要进行微分求导，但是数字图像是离散的，因此无法直接求导，可以利用一阶差分代替微分求离散图像的梯度大小和梯度方向，计算得到水平方向和垂直方向的梯度分别是，

$$ G_{h}(x, y)=f(x+1, y)-f(x-1, y),\forall x, y $$

$$ G_{v}(x, y)=f(x, y+1)-f(x, y-1) ,\forall x, y $$

其中表示图像在的像素值1。

可以得到梯度值(梯度强度)和梯度方向分别为,

$$ M(x, y)=\sqrt{G_{h}(x, y)^{2}+G_{v}(x, y)^{2}} $$

$$ \theta(x, y)=\arctan \left(G_{h}(x, y) / G_{v}(x, y)\right. $$

单元划分

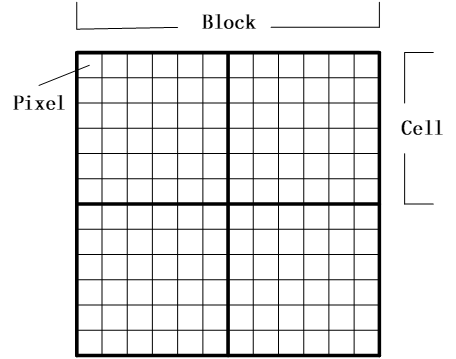
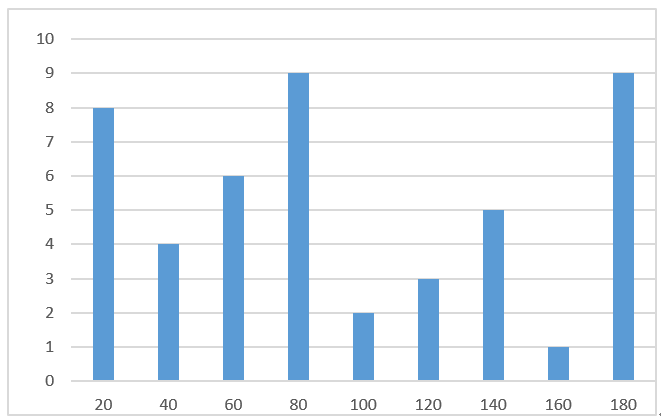
计算得到梯度的幅值和梯度方向之后，紧接着就是要建立分块直方图，得到图像的梯度大小和梯度方向后根据梯度方向对图像进行投影统计，首先将图像划分成若干个块(Block)，每个块又由若干个细胞单元(cell)组成，细胞单元由更小的单位像素(Pixel)组成，然后在每个细胞单元中对内部的所有像素的梯度方向进行统计。Dalal和Triggs通过测试验证得出，把方向分为9个通道效果最好，因此将180度划分成9个区间，每个区间为20度，如果像素落在某个区间，就将该像素的直方图累加在该区间对应的直方图上面，例如，如果像素的梯度方向在0~~20度之间，则在0~~20对应的直方图上累加该像素对应的梯度幅值。这样最终每个细胞单元就会得到一个9维的特征向量，特征向量每一维对应的值是累加的梯度幅值。

区块选择

为了应对光照和形变，梯度需要在局部进行归一化。这个局部的区块该怎么选择？常用的有两种，分别是矩形区块(R-HOG)和圆形区块(C-HOG)，前面提供的例子就是矩形区块，一个矩形区块由三个参数表示：每个区块由多少放歌、每个方格有多少像素、每个像素有多少通道。前面已经提到，经过作者验证，每个像素选择9个通道效果最佳。同样，作者对每个方格采用的像素数也进行验证，经过验证每个方格采用33或者66个像素效果较好。

区间归一化

每个方格内对像素梯度方向进行统计可以得出一个特征向量，一个区块内有多个方格，也就有多个特征向量，例如前面的示例区块Block内就有4个9维向量。这一步要做的就是对这4个向量进行归一化，Dalal和Triggs采用了四种不同的方式对区块进行归一化，分别是L2-norm、L2-hys、L1-norm、L1-sqrt，用表示未被归一化的向量，以L2-norm为例，归一化后的特征向量为，

$v=\frac{v}{\sqrt{|v|_{2}^{2}+\varepsilon^{2}}}$ v=\frac{v}{\sqrt{|v|_{2}^{2}+\varepsilon^{2}}}

作者通过对比发现，L2-norm、L2-hys、L1-sqrt三种方式所取得的效果是一样的，L1-norm表现相对差一些。

SVM分类器

最后一步，也是比较关键的一步，就是训练分类器，用SVM对前面提取的图像特征向量进行训练，寻找一个最优超平面作为决策函数，得到目标的训练模型。

编程实践

完整代码请查看：

https://github.com/Jackpopc/aiLearnNotes/blob/master/computer_vision/HOG.py

HOG是一个优秀的特征提取算法，因此本文就仅介绍并实现特征提取算法部分，后面的训练分类器和目标检测偏重于机器学习内容，在这里就不多赘述。

HOG算法非常经典，因此，很多成熟的第三方库都已经集成了这个算法，例如比较知名的计算机视觉库OpenCV，对于HOG特征提取比较简单的方式就是直接调用OpenCV库，具体代码如下，

import cv2
hog = cv2.HOGDescriptor()
img = cv2.imread("../data/2007_000129.jpg", cv2.IMREAD_GRAYSCALE)
des = hog.compute(img)

为了更好的理解HOG算法，本文就跟随文章的思路来重新实现一遍算法。

第一步：计算梯度方向和梯度幅值

这里用Sobel算子来计算水平和垂直方向的差分，然后用对梯度大小加权求和的方式来计算统计时使用的梯度幅值，

def compute_image_gradient(img):
    x_values = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5)
    y_values = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5)
    magnitude = cv2.addWeighted(x_values, 0.5, y_values, 0.5, 0)
    angle = cv2.phase(x_values, y_values, angleInDegrees=True)
    return magnitude, angle

第二步：统计细胞单元的梯度方向

指定细胞单元尺寸和角度单元，然后对用直方图统计一个细胞单元内的梯度方向，如果梯度角度落在一个区间内，则把该像素的幅值加权到和角度较近的一个角度区间内，

def compute_cell_gradient(cell_magnitude, cell_angle, bin_size, unit):
    centers = [0] * bin_size
    # 遍历细胞单元，统计梯度方向
    for i in range(cell_magnitude.shape[0]):
        for j in range(cell_magnitude.shape[1]):
            strength = cell_magnitude[i][j]
            gradient_angle = cell_angle[i][j]
            min_angle, max_angle, mod = choose_bins(gradient_angle, unit, bin_size)
            # 根据角度的相近程度分别对邻近的两个区间进行加权
            centers[min_angle] += (strength * (1 - (mod / unit)))
            centers[max_angle] += (strength * (mod / unit))
    return centers

第三步：块内归一化

根据HOG原文的思想可以知道，图像内分块，块内分细胞单元，然后对细胞单元进行统计。一个块由多个细胞单元组成，统计了每个细胞单元的梯度特征之后需要对这几个向量进行归一化，

def normalized(cell_gradient_vector):
    hog_vector = []
    for i in range(cell_gradient_vector.shape[0] - 1):
        for j in range(cell_gradient_vector.shape[1] - 1):
            block_vector = []
            block_vector.extend(cell_gradient_vector[i][j])
            block_vector.extend(cell_gradient_vector[i][j + 1])
            block_vector.extend(cell_gradient_vector[i + 1][j])
            block_vector.extend(cell_gradient_vector[i + 1][j + 1])
            mag = lambda vector: math.sqrt(sum(i ** 2 for i in vector))
            magnitude = mag(block_vector)
            if magnitude != 0:
                # 归一化
                normalize = lambda block_vector, magnitude: [element / magnitude for element in block_vector]
                block_vector = normalize(block_vector, magnitude)
            hog_vector.append(block_vector)
    return hog_vector

第四步：可视化

为了直观的看出特征提取的效果，对下图进行特征提取并且可视化，

可视化的方法是在每个像素上用线段画出梯度的方向和大小，用线段的长度来表示梯度大小，

def visual(cell_gradient, height, width, cell_size, unit):
    feature_image = np.zeros([height, width])
    cell_width = cell_size / 2
    max_mag = np.array(cell_gradient).max()
    for x in range(cell_gradient.shape[0]):
        for y in range(cell_gradient.shape[1]):
            cell_grad = cell_gradient[x][y]
            cell_grad /= max_mag
            angle = 0
            angle_gap = unit
            for magnitude in cell_grad:
                angle_radian = math.radians(angle)
                x1 = int(x * cell_size + magnitude * cell_width * math.cos(angle_radian))
                y1 = int(y * cell_size + magnitude * cell_width * math.sin(angle_radian))
                x2 = int(x * cell_size - magnitude * cell_width * math.cos(angle_radian))
                y2 = int(y * cell_size - magnitude * cell_width * math.sin(angle_radian))
                cv2.line(feature_image, (y1, x1), (y2, x2), int(255 * math.sqrt(magnitude)))
                angle += angle_gap
    return feature_image

提取的特征图为，图中白色的线段即为提取的特征，

完整代码如下，

import cv2
import numpy as np
import math
import matplotlib.pyplot as plt

img = cv2.imread("../data/2007_000129.jpg", cv2.IMREAD_GRAYSCALE)


def compute_image_gradient(img):
    x_values = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=5)
    y_values = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=5)
    magnitude = abs(cv2.addWeighted(x_values, 0.5, y_values, 0.5, 0))
    angle = cv2.phase(x_values, y_values, angleInDegrees=True)
    return magnitude, angle


def choose_bins(gradient_angle, unit, bin_size):
    idx = int(gradient_angle / unit)
    mod = gradient_angle % unit
    return idx, (idx + 1) % bin_size, mod


def compute_cell_gradient(cell_magnitude, cell_angle, bin_size, unit):
    centers = [0] * bin_size
    for i in range(cell_magnitude.shape[0]):
        for j in range(cell_magnitude.shape[1]):
            strength = cell_magnitude[i][j]
            gradient_angle = cell_angle[i][j]
            min_angle, max_angle, mod = choose_bins(gradient_angle, unit, bin_size)
            print(gradient_angle, unit, min_angle, max_angle)
            centers[min_angle] += (strength * (1 - (mod / unit)))
            centers[max_angle] += (strength * (mod / unit))
    return centers


def normalized(cell_gradient_vector):
    hog_vector = []
    for i in range(cell_gradient_vector.shape[0] - 1):
        for j in range(cell_gradient_vector.shape[1] - 1):
            block_vector = []
            block_vector.extend(cell_gradient_vector[i][j])
            block_vector.extend(cell_gradient_vector[i][j + 1])
            block_vector.extend(cell_gradient_vector[i + 1][j])
            block_vector.extend(cell_gradient_vector[i + 1][j + 1])
            mag = lambda vector: math.sqrt(sum(i ** 2 for i in vector))
            magnitude = mag(block_vector)
            if magnitude != 0:
                normalize = lambda block_vector, magnitude: [element / magnitude for element in block_vector]
                block_vector = normalize(block_vector, magnitude)
            hog_vector.append(block_vector)
    return hog_vector


def visual(cell_gradient, height, width, cell_size, unit):
    feature_image = np.zeros([height, width])
    cell_width = cell_size / 2
    max_mag = np.array(cell_gradient).max()
    for x in range(cell_gradient.shape[0]):
        for y in range(cell_gradient.shape[1]):
            cell_grad = cell_gradient[x][y]
            cell_grad /= max_mag
            angle = 0
            angle_gap = unit
            for magnitude in cell_grad:
                angle_radian = math.radians(angle)
                x1 = int(x * cell_size + magnitude * cell_width * math.cos(angle_radian))
                y1 = int(y * cell_size + magnitude * cell_width * math.sin(angle_radian))
                x2 = int(x * cell_size - magnitude * cell_width * math.cos(angle_radian))
                y2 = int(y * cell_size - magnitude * cell_width * math.sin(angle_radian))
                cv2.line(feature_image, (y1, x1), (y2, x2), int(255 * math.sqrt(magnitude)))
                angle += angle_gap
    return feature_image


def main(img):
    cell_size = 16
    bin_size = 9
    unit = 360 // bin_size
    height, width = img.shape

    magnitude, angle = compute_image_gradient(img)

    cell_gradient_vector = np.zeros((height // cell_size, width // cell_size, bin_size))
    for i in range(cell_gradient_vector.shape[0]):
        for j in range(cell_gradient_vector.shape[1]):
            cell_magnitude = magnitude[i * cell_size:(i + 1) * cell_size,
                             j * cell_size:(j + 1) * cell_size]
            cell_angle = angle[i * cell_size:(i + 1) * cell_size,
                         j * cell_size:(j + 1) * cell_size]
            cell_gradient_vector[i][j] = compute_cell_gradient(cell_magnitude, cell_angle, bin_size, unit)
    hog_vector = normalized(cell_gradient_vector)
    hog_image = visual(cell_gradient_vector, height, width, cell_size, unit)
    plt.imshow(hog_image, cmap=plt.cm.gray)
    plt.show()


if __name__ == '__main__':
    img = cv2.imread('../data/2007_002293.jpg', cv2.IMREAD_GRAYSCALE)
    cv2.imshow("origin", img)
    cv2.waitKey()
    main(img)

2.5 DPM模型

前言

DPM(Deformable Part Model)模型，又称为可变型部件模型，是Felzenszwalb于2008年提出的一个模型。这可以说是传统目标识别算法中最为经典的算法之一，我认为对计算机视觉有一些深入了解的同学应该对DPM模型都有所耳闻。

首先说一下DPM模型这篇文章有多牛。DPM模型的作者Felzenszwalb凭借这个模型一举获得2010年voc挑战赛的终身成就奖，感觉还是不够牛？不知道Felzenszwalb是何许人也？Felzenszwalb正是Ross B. Girshick(也就是DPM模型的第二作者)硕士和博士期间的导师。我想，如果连Ross B. Girshick都不知道的话就真的称不上是一个计算机视觉领域的学习者了。它正是R-CNN系列、YOLO系列等现如今被奉为经典的计算机视觉模型的提出者或共同提出者，可以说是这几年计算机视觉领域比较有作为的一位研究者。

说完DPM的作者很牛，那和DPM有什么关系？前面提到，它的作者是近几年计算机视觉领域非常知名的研究者，因此，自然而然，这几年比较成功的计算机视觉模型都会受到这个标杆性算法的影响。多尺度、锚点、可变型部件，都对后面深度学习计算机视觉带了巨大的影响。

介绍完DPM模型的背景，再回到这个算法本身。DPM模型和前文讲到的HOG整体流程非常类似，HOG采用HOG特征加linear SVM，而DPM采用多尺度特征加latent SVM，此外，DPM在特征提取方面也是在HOG特征的基础上进行稍加改进。虽然从文中看上去两者差别并不大，但是其实DPM无论是在特征提取层面还是在机器学习层面都做了巨大的改进。

首先是特征提取思想，HOG模型仅仅考虑根模型的特征，不考虑部件模型的特征，而DPM模型采用根模型加部件模型的思路，同时考虑外观和细节部分的特征。

其次是SVM方面，Latent SVM加入了潜在信息的训练。

下面就分别从特征提取到模型训练介绍一下这个模型。

特征提取

文章中讲的有点让新学者难以理解，这里我就对照着HOG特征讲解一下，更有助于理解。

两者相同的是第一步都要先计算梯度方向，然后对梯度方向进行统计。

不同之处是，HOG特征含有块(block)的概念，它首先把一副图像划分成若干个块，然后再把块划分成若干个单元，然后对单元内部的像素进行梯度统计，然后对同一个块内的特征向量进行归一化，HOG采用的是0~180度之间的梯度方向，20度一个区间，这样每个细胞单元就统计得到一个9维特征向量，一个块内就得到n * 9维特征向量。

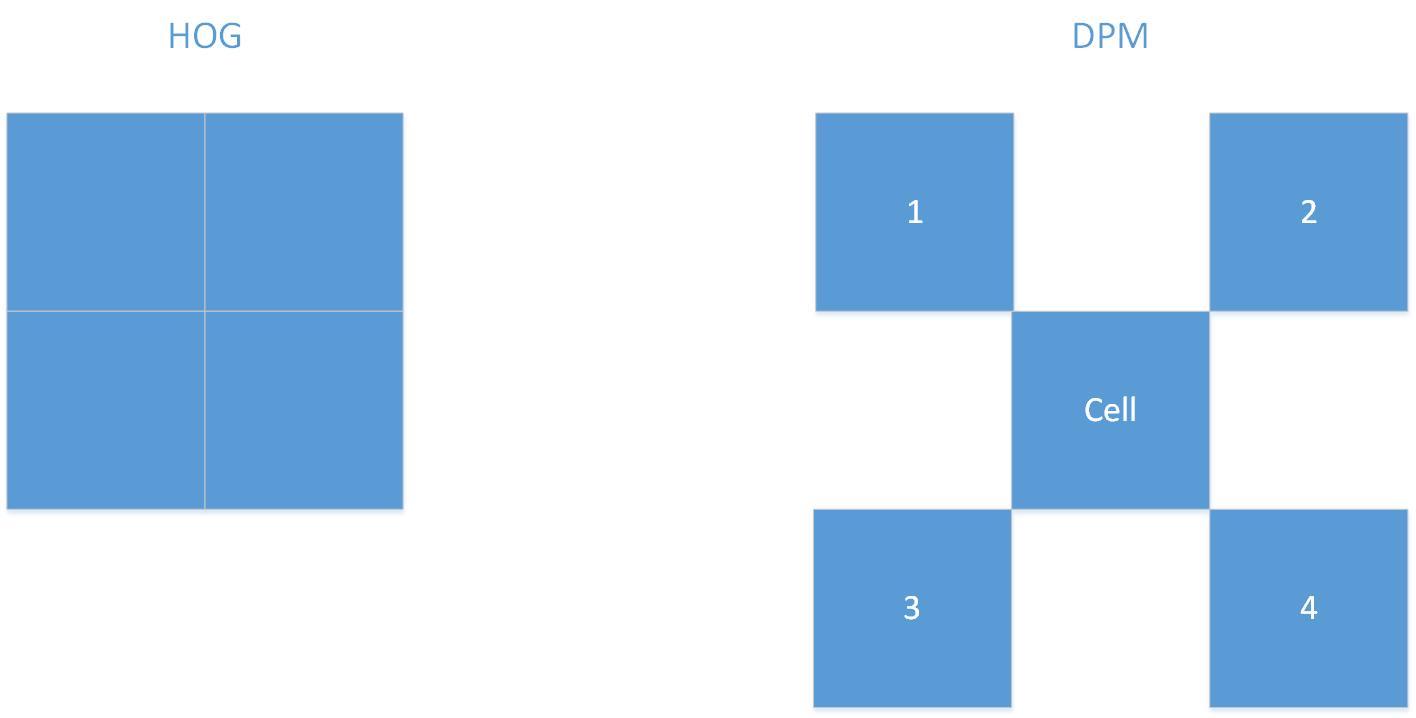
由于HOG采用的梯度方向为0180度方向不敏感特征，这样会丢失很多特征信息，DPM模型对HOG做了很大的改进。首先DPM模型没有快的概念，它是去一个细胞单元四角对应的领进单元的特征进行归一化，此外，更重要的是DPM不仅提取结合0180度方向不敏感特征和0~~360度方向敏感特征两种特征，它首先提取0~~180度之间的特征，得到上图所示4*9维的特征，拼接起来得到13维特征向量，然后再提取0~360度之间的特征，得到18维特征向量，二者相加得到31维特征向量。

模型训练

前面介绍了一下DPM模型特征提取的方法，虽然思想与HOG有很大不同之处，但是在最基本的梯度方向统计方面是相同的。

知道了如何从一副图像中提取我们想要的特征，要进一步深入理解一个算法，我认为从模型训练、模型预测方面是最简单明了的方法，无论是传统目标识别还是深度计算机视觉。知道它是如何训练、如何预测的就知道这个模型的运作情况，输入是什么？中间经历了什么过程？输出是什么？下面就来看一下DPM模型的训练过程。

本算法采用的训练说句来自于Pascal VOC，用过这个数据集的都知道，它只标记了图片中目标的包围合，并没有标记图像的部件，例如它只标记了一个人，并没有标记人的胳膊、腿、头部等，而DPM被称为可变型部件模型，那么部件体现在哪里？怎么知道它的部件在哪？下面来了解一下它的训练过程，能够帮助理解这个算法。

DPM的在训练之前先进性了初始化，主要包括3个阶段：

初始化根滤波器

为了训练一个有m个组件的混合模型，首先将正样本按照长宽比划分成m组，然后针对每一组训练一个根滤波器F1、F2、...、Fm，在训练根模型过程中使用的是标准的SVM，不含有潜在信息，例如上图(a)、(b)就是初始化的两个根模型。

合并组件

把初始化的根滤波器合并到一个没有部件的混合模型中并且重新训练参数，在这个过程中，组件的标签和根的位置是潜在变量(组件和部件不是同一个概念)。

初始化部件滤波器

前面提到，数据集中并没有标记部件的位置，因此文中在初始化部件滤波器是用了一个简单的假设，将每个组件的部件数量固定在6个，并使用一个矩形部件形状的小池，文中贪婪地放置部件，以覆盖根过滤器得分较高的区域。

另外需要清楚的是，部件滤波器是在根据滤波器2倍分辨率的图像上进行初始化，因为分辨率越高，细节越清晰，越能提取部件的特征。

经过初始化之后就可以训练模型参数。

下面是详细的训练过程，

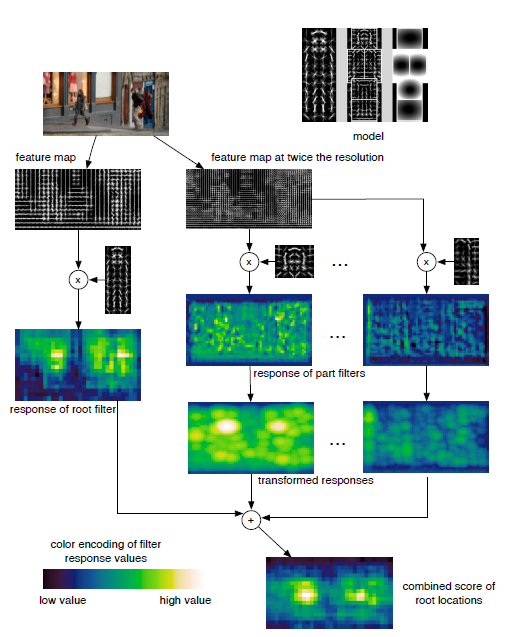
模型检测

前面介绍了DPM模型的特征提取和训练过程，下面就来看一下模型检测过程。

上述就是就是DPM模型检测的详细过程：

对输入图像进行特征提取，得到特征图和2倍分辨率的特征图
分别在特征图和2倍分辨率上计算根滤波器和部件滤波器的得分
合并根位置的得分，得到总得分

用数学语言表示，图像的总得分为，

$$ \begin{array}{l}{\operatorname{score}\left(x_{0}, y_{0}, l_{0}\right)=} {\quad R_{0, l_{0}}\left(x_{0}, y_{0}\right)+\sum_{i=1}^{n} D_{i, l_{0}-\lambda}\left(2\left(x_{0}, y_{0}\right)+v_{i}\right)+b}\end{array} $$

模型检测过程就是获取局部最大响应(得分)的过程，前面已经训练得到了$R_{0, l_{0}}\left(x_{0}, y_{0}\right)$是根滤波器的得分，$\sum_{i=1}^{n} D_{i, l_{0}-\lambda}\left(2\left(x_{0}, y_{0}\right)+v_{i}\right)$是部件滤波器的得分，$b$ 是偏移量。

Latent SVM

在经典的SVM中，认为训练样本的标记是严格符合类别标签的，标记的正样本就是正样本、标记负样本就是负样本，但是由于标记过程中有很多人为因素，因此，虽然能保证负样本一定是负的，但是却不能保证正样本一定属于正的。因此在训练过程中有很多潜在的未知信息，作者发现，将根位置作为一个潜在变量，可以有效地补偿正样本中存在噪声的边界框标签。

Latent SVM训练的目标函数为，

$$ L_{D}(\beta)=\frac{1}{2}|\beta|^{2}+C \sum_{i=1}^{n} \max \left(0,1-y_{i} f_{\beta}\left(x_{i}\right)\right) $$

其中 ,

$$ f_{\beta}(x)=\max _{z \in Z(x)} \beta \cdot \Phi(x, z) $$

$z$是潜在信息。

源码解析

由于DPM模型工程量较大，而且作者已经开源代码并且经过多个版本的迭代，目前非常成熟，因此不在这里逐步实现，在这里主要讲解一下怎么使用源码去检测目标和训练模型。

目前源码版本为 voc-release5，可以直接访问官网下载，

http://www.rossgirshick.info/latent/

也可以关注公众号回复voc获取。

DPM的源码是由Matlab和C++进行混编而成，Matlab主要用于做一些简单的图像处理，由于在模型训练和特征提取过程中非常缓慢，因此，为了提高效率，作者用C++实现了特征提取和模型训练部分，另外，由于C++部分使用了一些多线程的库，所以在windows下无法直接运行，需要做一些修改，在linux和mac下可以直接运行。

目标检测

用训练好的模型检测目标，主要有如下几个步骤，

解压缩代码。
运行Matlab。
运行'compile'函数来编译helper函数。
加载模型和图像。
检测目标。

示例，

>> load VOC2007/car_final.mat;      
>> im = imread('000034.jpg');        
>> bbox = process(im, model, -0.5);  
>> showboxes(im, bbox);

训练模型

可以自己按照voc的格式准备数据，训练自己的模型，去检测相应的目标，详细过程如下，

下载数据集和VOC devkit工具包。
根据自己的数据配置voc_config.m。
运行'compile'函数来编译helper函数。
利用pascal.m脚本训练模型

示例，

>> pascal('bicycle', 3);

第三章卷积神经网络

3.1 卷积神经网络综述

个人主页>>

GitHub>>

前言

提起卷积神经网络(CNN)，应该很多人都有所耳闻。自从2012年AlexNet在ImageNet挑战赛一举夺魁，它再一次的回到的人们的视野。

为什么称之为"再一次"，因为CNN并不是近几年的产物，早在20世纪90年代Yann LeCun就提出了最基础的卷积神经网络模型(LeNet)，但是由于算力和数据的限制，它一直处于一种被冷遇的地位，传统目标识别方法，例如之前所讲到的SIFT、HOG、DPM占据着不可撼动的统治地位。

但是随着算力的提升和数据集的积累，这一切都变了，在AlexNet成功之后，CNN如同雨后春笋一样，每年各种各样的Net数不胜数，近其中知名的就有AlexNet、VGG、GoogleNet、UNet、R-CNN、FCN、SSD、YOLO等。

入门计算机视觉领域的绝大多数同学应该都学过或听说过斯坦福大学的公开课(CS231n: Convolutional Neural Networks for Visual Recognition)，主要就围绕CNN进行展开，甚至很多近几年入门计算机视觉的同学就斩钉截铁的认为，计算机视觉就是卷积神经网络，我认为这有一些"一叶障目，不见泰山的"感觉。

CNN只是计算机视觉的一个子集，而且是一个很小的子集，更确切的说，计算机视觉是一种应用性技术，CNN是一种工具。

但是，不可否认，CNN是目前阶段我们能力所达到的、在大多数CV方向应用最为成功的一项技术，尤其是R-CNN系列和YOLO系列，在商业中，例如交通监测、车站安检、人脸识别应用非常多，效果对比于传统目标识别算法也要好很多，所以，它是学习计算机视觉中非常重要的一环，本文就概述一下近年来比较成功的CNN模型。本文只是用简略的语言进行概述，后续会挑选一些比较经典的模型进行详解和编程实现。

卷积神经网络概述

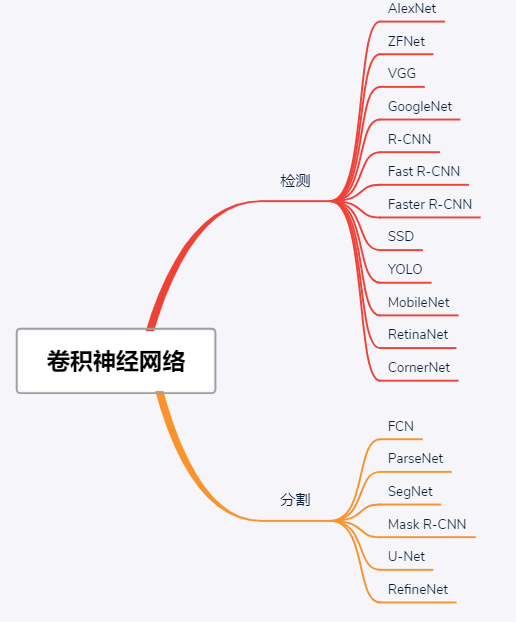
按功能对卷积神经网络进行分类主要可以分为两类，

检测(detection)
分割(segmentation)

检测的目的是要判断一副图像中是否有特定的目标，以及它所在的位置，通过一些手段识别出它所在的包围合区域。

分割的目的要更加严格一些，它不仅要识别出目标的所在区域，还要分割出目标的边缘，尤其在CNN图像分割领域，和传统的图像分割不同，它不能简单的依靠梯度变化幅度把目标分割出来，还需要进行语义上的分割，识别到像素级的类别。

目前比较知名的用于识别的CNN模型有，

AlexNet
VGG
R-CNN系列
Resnet
MobileNet
YOLO系列

在分割方面比较知名的CNN模型有，

Mask R-CNN
FCN
U-Net
SegNet

CNN中主要用到的技术

系统学习以上上述所提到的知名CNN模型会发现，其中所使用到的技术手段大同小异，而那些知名度较小的CNN模型更是如此，创新点更是微乎其微，其中所使用到的技术主要有，

卷积
池化
基础块
Dropout
跳跃连接
锚点
优化算法
激活函数
批量正则化
回归

卷积和池化是非常基础的，在特征提取过程中至关重要。

基础块的思想最初出自于VGG，它在AlexNet的基础上进行了很大的改进，基础块思想的引入增加了网络的重用性，后续很多模型都死在这一举出上进行改进的，因此，在很多后续的网络模型都是以VGG为基础模型。

Dropout这个几乎成了CNN模型中必不可少的一个组件，它在应对过拟合问题中具有非常重要的价值。

跳跃连接最初出现在ResNet，在网络的不断改进中发现，其中的思想都是使网络越来越深，网络适当的加深的确能够带来识别精度的提到，但是真的越深越好吗？当然不是。随着网络的加深，很容易出现梯度消失和梯度爆炸现象，ResNet中提出的跳跃连接在后来的网络模型中扮演者非常重要的角色。

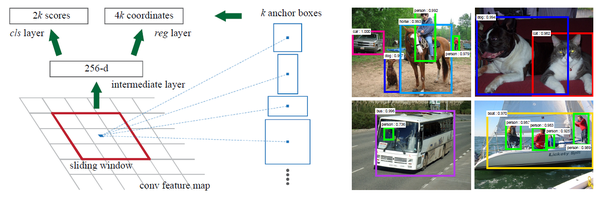
锚点这一概念最初是在2008年的DPM模型中看到，后来Faster R-CNN中主要的使用了这项技术，使得它名声大噪，后来的经典模型几乎都用到了锚点这个思想。

优化算法对于上述CNN模型的价值自然不言而喻，梯度下降、Adam、牛顿法等，可以说这是深度计算机视觉的核心所在，也是理论体系最完善、最能够用数学模型解释的一部分。

激活函数和Dropout一样，也是CNN模型中必不可少的一个组件，它的主要价值在于解决模型的线性不可分问题，把非线性的特性引入到网络模型中。

批量正则化也是CNN中常用的一个功能，它的主要作用是加速模型的收敛，避免深层神经网络的梯度消失和梯度爆炸。

回归中用到的较多的自然是softmax，它将经过各种网络层处理得到的特性向量进行回归，得到每一个类别对应的概率，在多分类问题中是一个必不可少的功能。

CNN模型架构

纵观上述所提及的经典CNN模型，它们的模型架构非常相似，主要包含如下几个部分：

输入层
特征提取层
全连接层
回归
输出层

输入层主要是用于读取图像，用于后面的网络层使用。

特征提取层主要通过卷积来获取图像局部的特征，得到图像的特征图。

全连接层用于对特征层进行后处理，然后用于回归层处理。

回归主要通过一些回归函数，例如softmax函数来对前面得到的特征向量进行处理，得到每个类别对应的概率。

输出层用于输出检测和分类的结果。

当然，在这个过程中某些环节会用到上述提到的激活函数、批量正则化、优化算法以及非极大值抑制。

搭建CNN目标识别系统

有了上述强大的模型，在实际项目中该怎么搭建一个有价值的CNN目标识别系统呢？我认为主要分为如下几个步骤，

数据获取
数据预处理
模型搭建
数据后处理

在CNN，乃至整个深度学习领域都可以说数据获取是至关重要的一部分，甚至可以说占据了超过50%的地位。深度学习的发展主要就是得益于这么多年来数据的积累，很多项目和工程也是由于数据的限制和却是只能中途作废。因此，数据获取部分是搭建目标识别系统中最重要的一个环节，它直接决定着是否能够继续走下去。

目前有一些公开的数据集可以获取，例如MNIST、Pascal VOC、ImageNet、Kaggle等。如果自己所做的方向恰好巧合，这些公开数据集里有相应的数据，那么的确是幸运的，可以从这些数据中直接获取。

数据预处理对于CNN同样非常重要，各种视频、摄像头在数据采集的过程中很难保证数据是有价值的，或者干净的，这里就需要对数据进行去噪、去模糊、增强分辨率，如果数据集不充足，还需要对数据进行扩充。

模型搭建我认为是这几个环节中相对较为容易的一部分，首先目前这些经典的框架都有开源的项目，有的甚至不止一个版本，我们可以借鉴甚至直接拿来用这些模型。即便不愿意选择开源的项目，也可以使用tensorflow、pytorch进行搭建，其中需要的代码量是非常有限的。

输出检测的结果需要进行非极大值抑制、绘出包围合等后续工作，以及和一些系统进行对接，这样它才是一个可用的完整系统。

3.2 卷积层、池化层与填充

前言

从2012年AlexNet成名之后，CNN如同雨后春笋一样，出现了各种各样的Net，其中也有很多知名的，例如VGG、GoogleNet、Faster R-CNN等，每个算法都在前面研究工作的基础上做出了很大的改进，但是这些CNN模型中主要使用的组件却有很多重叠之处，这个组件主要有：

卷积层
池化层
激活函数
优化函数
全连接层
Dropout
批量正则化
填充padding
......

其实一个CNN网络的模型搭建过程非常容易，现在有很多优秀的机器学习框架，例如tensorflow、pytorch、mxnet、caffe、keras等，借助这些机器学习框架搭建一个CNN网络模型只需要几十行代码即可完成，而且使用到的函数屈指可数，难度并不大。而上述提到的这些组件却是CNN中非常核心的概念，了解它们是什么？有什么价值？在哪里起作用？掌握这些之后再回头看这些CNN模型就会发现轻而易举，因此，这几节会先把上述这些技术介绍一下，然后逐个讲解如何一步一步搭建那些成熟优秀的CNN模型。

由于上述每个技术都涉及很多知识点，本文为了效率就用简单的语言介绍它是什么？有什么价值？具体详细的内容可以阅读文章或者外网资料详细了解，本文主要介绍3点：

卷积层
池化层
填充padding

卷积层

介绍

卷积神经网络(convolutional neural network)，从它的名称就可以看出，卷积是其中最为关键的部分。在前面讲解图像去噪和图像分割中提到了一些用于分割和去噪的算法，例如sobel算子、中值滤波，其实卷积的概念和这些有相同之处。

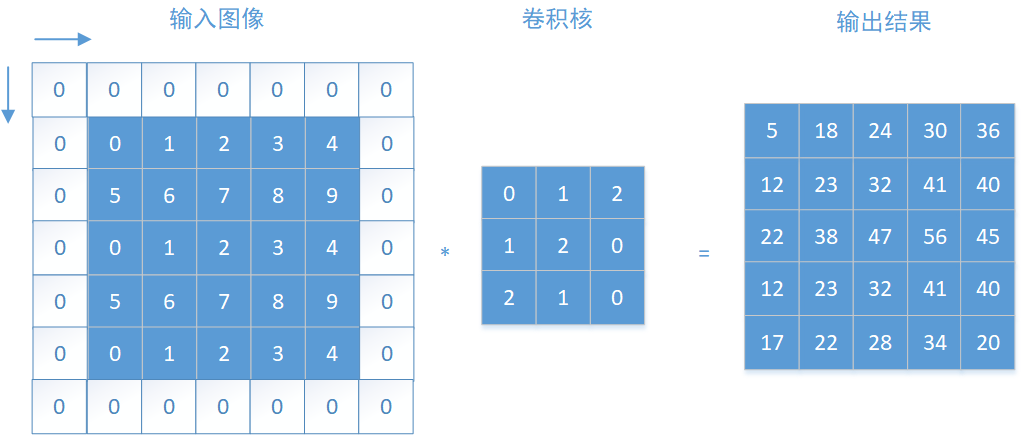
把输入图像看作是一个n维矩阵，然后拿一个m*m维(m<n)的卷积核(或者称为滤波器)，从图像的左上角开始沿着从左至右、从上之下进行"扫描"，每当移动到一个窗口后和对应的窗口做卷积运算(严格的说是互相关运算)，用直白的话来说就是对应元素相乘之后加和。

移动过程中涉及一个重要的概念--步长(stride)，它的意思就是"扫描"过程中每次移动几个像素，如果步长stride=1，那么从左至右、从上之下逐个像素的移动。

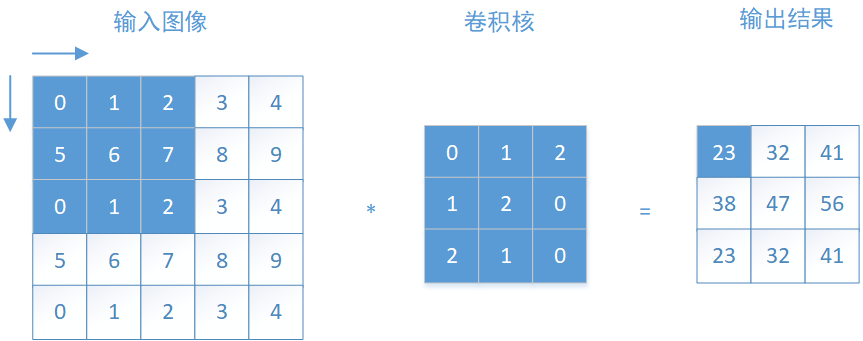
以上图二维卷积运算为例，输入图像为一个55的矩阵，卷积核为33，以步长stride=1进行卷积运算，在左上角这个窗口每个对应元素先相乘再加和，即，

$$ 00+11+22+15+26+07+20+11+0*2=23 $$

以这种方式逐个窗口进行计算，就得到图中等号右边的输出结果。

tensorflow使用

在tensorflow中关于卷积层的函数为，

tensorflow.nn. conv2d(input, filter, strides, padding)

其中参数分别为：

input：输入数据或者上一层网络输出的结果
filter：卷积核，它的是一个1*4维的参数，例如filter=[5, 5, 3, 96]，这4个数字的概念分别是卷积核高度、卷积核宽度、输入数据通道数、输出数据通道数
strides：这是前面所讲的步伐，同卷积核一样，它也是一个1*4维的参数，例如strides=[1, 2, 2, 1]，这4个数字分别是batch方向移动的步长、水平方向移动的步长、垂直方向移动的步长、通道方向移动的步长，由于在运算过程中是不跳过batch和通道的，所以通常情况下第1个和第4个数字都是1
padding：是填充方式，主要有两种方式，SAME, VALID，后面会讲什么是填充

池化层

介绍

池化层和卷积层一样，是CNN模型必不可少的一个部分，在很多卷积层后会紧跟一个池化层，而且在统计卷积神经网络时，池化层是不单独称为网络层的，它与卷积层、激活函数、正则化同时使用时共同称为1个卷积层。

池化层又成为下采样或者欠采样，它的主要功能是对于特征进行降维，压缩数据和参数量，避免过拟合，常用的池化方式有两种：

最大池化
平均池化

以最大池化为例介绍一下它是怎么实现的，

和卷积层类似，池化层也有窗口和步长的概念，其中步长在里面的作用也是完全相同的，就是窗口每次移动的像素个数，所以不再赘述。

池化层的窗口概念和卷积层中是截然不同的，在卷积层中每移动到一个窗口，对应的卷积核和输入图像做卷积运算。而在池化层中，窗口每移动到一个位置，就选择出这个窗口中的最大值输出，如果是平均池化就输出这个窗口内的平均值。

tensorflow使用

tensorflow中池化运算的函数为，

tensorflow.nn.max_pool(value, ksize, strides, padding)

从函数的参数即可看出来，它和卷积层非常相似，它的参数概念分别是，

value：输入数据或者上一层网络输出的结果
ksize：卷积核，它的是一个1*4维的参数，例如ksize=[1, 3, 3, 1]，这4个数字的概念分别是batch维度池化窗口、池化窗口高度、池化窗口宽度、通道维度窗口尺寸，由于在batch和通道维度不进行池化，所以通常情况下第1和第4个元素为1
strides：这和卷积层中相同
padding：这和卷积层中的也相同

填充

在前面讲解卷积层和池化层时都提到了一个概念--填充，可见它是非常重要的。什么是填充？SAME, VALID这两种填充方式又有什么区别？下面来介绍一下。

从前面卷积层和池化层可以看出，卷积层和池化层的输出尺寸大小和选取的窗口大小有着密切关系，以卷积层为例，上述输入为55，但是输出为33，输出尺寸变小了，而且在输入图像的四周的元素只被卷积了一次，中间的元素却被利用多次，也就是说，如果是一副图像，图像四周的信息未被充分提取，这就体现了填充的价值，

保持边界信息
使得输入输出图像尺寸一致

那怎么样达到上述这2个目的？就是通过填充，一般情况下是在图像周围填充0，如下，

如上图所示，在输入图像周围填充0，然后通过卷积运算，输入和输出的尺寸都为55。当然，这是针对卷积核为33情况下，外层填充1层，具体填充几层，要根据卷积核大小而定。

然后回到前面所提到的，tensorflow中填充padding参数有两个选项：SAME, VALID，它们有什么区别呢？

VALID：不进行填充

SAME：填充0，使得输出和输入的尺寸相同，就如同上面这个例子。

3.3 激活函数

前言

激活函数不仅对于卷积神经网络非常重要，在传统机器学习中也具备着举足轻重的地位，是卷积神经网络模型中必不可少的一个单元，要理解激活函数，需要从2个方面进行讨论：

什么是激活函数？
为什么需要激活函数？

什么是激活函数？

对于神经网络，一层的输入通过加权求和之后输入到一个函数，被这个函数作用之后它的非线性性增强，这个作用的函数即是激活函数。

为什么需要激活函数？

试想一下，对于神经网络而言，如果没有激活函数，每一层对输入进行加权求和后输入到下一层，直到从第一层输入到最后一层一直采用的就是线性组合的方式，根据线性代数的知识可以得知，第一层的输入和最后一层的输出也是呈线性关系的，换句话说，这样的话无论中加了多少层都没有任何价值，这是第一点。

第二点是由于如果没有激活函数，输入和输出是呈线性关系的，但是现实中很多模型都是非线性的，通过引入激活函数可以增加模型的非线性，使得它更好的拟合非线性空间。

目前激活函数有很多，例如阶跃函数、逻辑函数、双曲正切函数、ReLU函数、Leaky ReLU函数、高斯函数、softmax函数等，虽然函数有很多，但是比较常用的主要就是逻辑函数和ReLU函数，在大多数卷积神经网络模型中都是采用这两种，当然也有部分会采用Leaky ReLU函数和双曲正切函数，本文就介绍一下这4个激活函数长什么样？有什么优缺点？在tensorflow中怎么使用？

Sigmoid

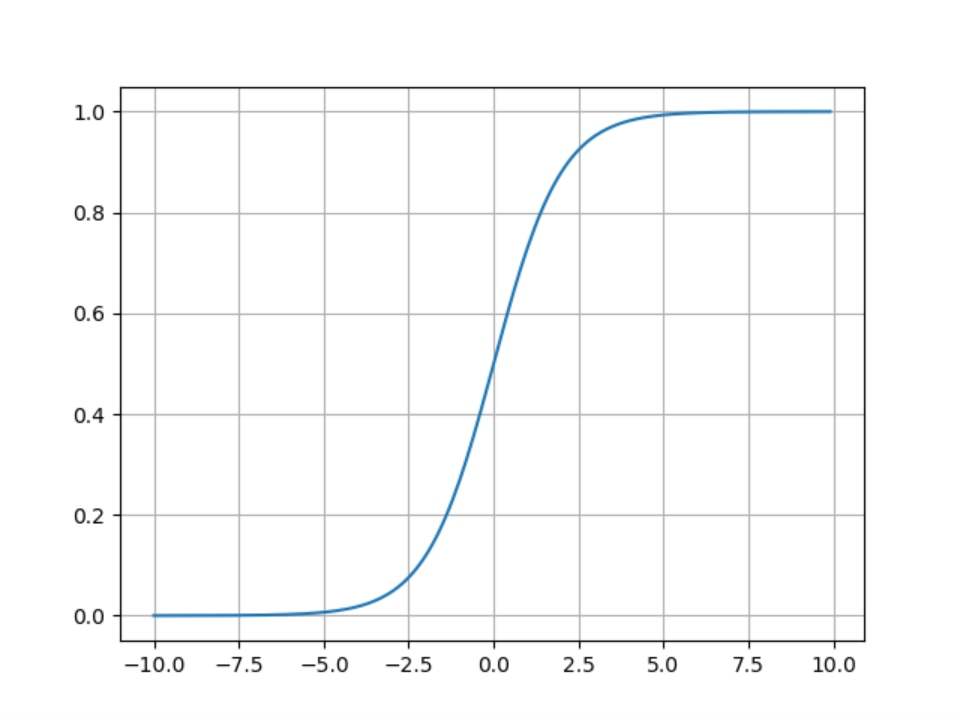
Sigmoid函数的方程式

绘图程序：

def sigmoid():
    x = np.arange(-10, 10, 0.1)
    y = 1 / (1+np.exp(-x))
    plt.plot(x, y)
    plt.grid()
    plt.show()

Sigmoid函数就是前面所讲的逻辑函数，它的主要优点如下：

能够将函数压缩至区间[0, 1]之间，保证数据稳定，波动幅度小
容易求导

缺点：

函数在两端的饱和区梯度趋近于0，当反向传播时容易出现梯度消失或梯度爆炸
输出不是0均值(zero-centered)，这样会导致，如果输入为正，那么导数总为正，反向传播总往正方向更新，如果输入为负，那么导数总为负，反向传播总往负方向更新，收敛速度缓慢
对于幂运算和规模较大的网络运算量较大

双曲正切函数

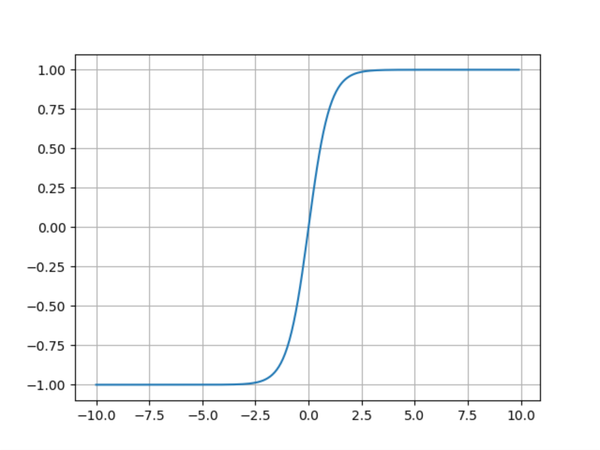
双曲正切函数方程式：

绘图程序：

def tanh():
    x = np.arange(-10, 10, 0.1)
    y = (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
    plt.plot(x, y)
    plt.grid()
    plt.show()

可以看出，从图形上看双曲正切和Sigmoid函数非常类似，但是从纵坐标可以看出，Sigmoid被压缩在[0, 1]之间，而双曲正切函数在[-1, 1]之间，两者的不同之处在于，Sigmoid是非0均值(zero-centered)，而双曲是0均值的，它的相对于Sigmoid的优点就很明显了：

提高了训练效率

虽然双曲正切函数解决了Sigmoid函数非0均值的问题，但是它依然没有解决Sigmoid的两位两个问题，这也是tanh的缺点：

梯度消失和梯度爆炸
对于幂运算和规模较大的网络运算量较大

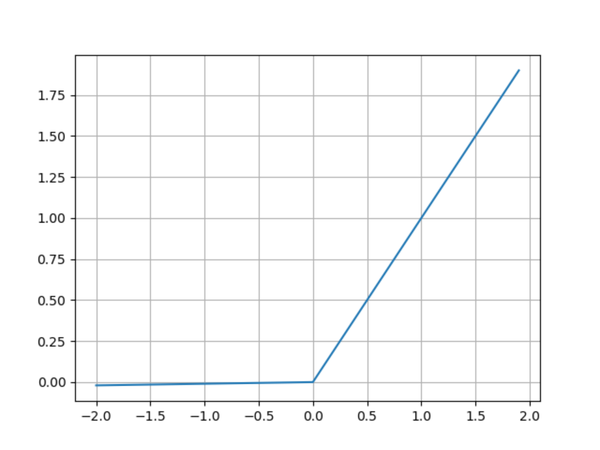
ReLU

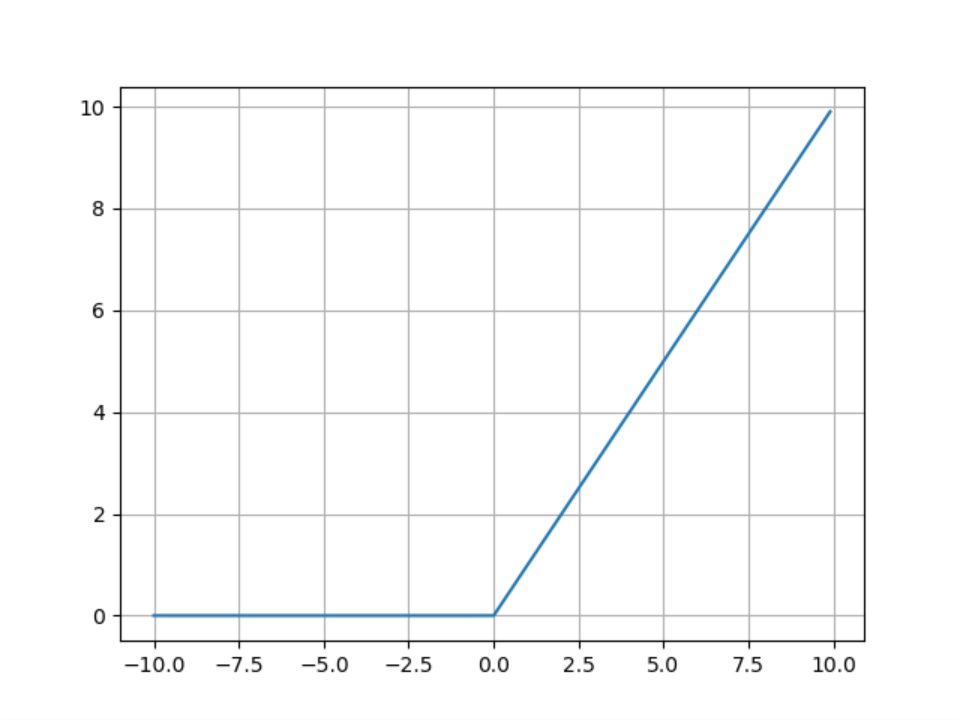
ReLU函数方程式：

绘图程序：

def relu():
    x = np.arange(-10, 10, 0.1)
    y = np.where(x<0, 0, x)
    plt.plot(x, y)
    plt.grid()
    plt.show()

线性整流函数(Rectified Linear Unit，ReLU)，对比于Sigmoid函数和双曲正切函数的优点如下：

梯度不饱和，收敛速度快
减轻反向传播时梯度弥散的问题
由于不需要进行指数运算，因此运算速度快、复杂度低

虽然解决了Sigmoid和双曲正切函数的缺点，但是它也有明显的不足：

输出不是0均值(zero-centered)
对参数初始化和学习率非常敏感，设置不当容易造成神经元坏死现象，也就是有些神经元永远不会被激活(由于负部梯度永远为0造成)

Leaky ReLU

Leaky ReLU函数方程式：

绘图程序：

def leaky_relu():
    x = np.arange(-2, 2, 0.1)
    y = np.where(x<0, 0.01*x, x)
    plt.plot(x, y)
    plt.grid()
    plt.show()

为了解决ReLU函数神经元坏死现象，Leaky ReLU函数在输入为负是引入了一个(0, 1)之间的常数，使得输入为负时梯度不为0。虽然Leaky ReLU解决了ReLU的这个严重问题，但是它并不总是比ReLU函数效果好，在很多情况下ReLU函数的效果还是更胜一筹。

tensorflow激活函数使用

tensorflow中激活函数在tf.nn模块下，例如，

tf.nn.relu
tf.nn.sigmoid
tf.nn.tanh
tf.nn.leaky_relu

其中relu、sigmoid、tanh函数的参数完全相同，leaky_relu多一个输入参数，就是斜率，默认值为0.2，以relu函数为例介绍一下tensorflow中激活函数的使用，

features = tf.nn.max_poo()
tf.nn.relu(features, name=None)

tensorflow中激活函数输入有两个参数：

features：输入的特征张量，也就是前一层池化层或者卷积层输出的结果，数据类型限制在float32, float64, int32, uint8, int16, int8, int64, float16, uint16, uint32, uint64
name：运算的名称，这个可以自行命名

3.4 批量归一化

前言

当我们用一些数据做一个预测系统时，我们首先需要对数据进行预处理，例如标准化、正则化、滑动窗口等，比如常用的Z-score、最大最小标准化，它能将数据转化为同一个量级，这样的话能够保证数据的稳定性、可比性。

这些标准化方法在浅层神经网络中已经足够使用，效果已经很不错。但是在深度学习中，网络越来越深，使用这些标准化方法就难以解决相应的问题。

为什么需要批量归一化？

在训练过程中，每层输入的分布不断的变化，这使得下一层需要不断的去适应新的数据分布，在深度神经网络中，这让训练变得非常复杂而且缓慢。对于这样，往往需要设置更小的学习率、更严格的参数初始化。通过使用批量归一化(Batch Normalization, BN)，在模型的训练过程中利用小批量的均值和方差调整神经网络中间的输出，从而使得各层之间的输出都符合均值、方差相同高斯分布，这样的话会使得数据更加稳定，无论隐藏层的参数如何变化，可以确定的是前一层网络输出数据的均值、方差是已知的、固定的，这样就解决了数据分布不断改变带来的训练缓慢、小学习率等问题。

在哪里使用批量归一化？

批量归一化是卷积神经网络中一个可选单元，如果使用BN能够保证训练速度更快，同时还可以具备一些正则化功能。

在卷积神经网络中卷积层和全连接层都可以使用批量归一化。

对于卷积层，它的位置是在卷积计算之后、激活函数之前。对于全连接层，它是在仿射变换之后，激活函数之前，如下所示：

conv_1 = tf.nn.conv2d()
norm_1 = tf.nn.batch_normalization(conv_1)
relu_1 = tf.nn.relu(norm_1)
pool_1 = tf.nn.max_pool(relu_1)

以卷积层为例，网络架构的流程为：

卷积运算
批量归一化
激活函数
池化

批量归一化

在讲批量归一化之前，首先讲一下数据标准化处理算法Z-score。

Z-score标准化也成为标准差标准化，它是将数据处理成均值为0，方差为1的标准正态分布，它的转化公式为，

$$ x^{*}=\frac{x-\overline{x}}{\sigma} $$

其中是处理前的数据，是处理后的数据，是原始数据的均值，是原始的标准差。这样的话就可以把数据进行标准化。

其实批量归一化在思想上和Z-score是有很多共通之处的。

在深度学习训练过程中会选取一个小批量，然后计算小批量数据的均值和方差，

$$ \boldsymbol{\mu}{\mathcal{B}} \leftarrow \frac{1}{m} \sum{i=1}^{m} \boldsymbol{x}^{(i)} $$

$$ \sigma_{\mathcal{B}}^{2} \leftarrow \frac{1}{m} \sum_{i=1}^{m}\left(\boldsymbol{x}^{(i)}-\boldsymbol{\mu}_{\mathcal{B}}\right)^{2} $$

然后对数据进行归一化处理，

$$ \hat{\boldsymbol{x}}^{(i)} \leftarrow \frac{\boldsymbol{x}^{(i)}-\boldsymbol{\mu}{\mathcal{B}}}{\sqrt{\boldsymbol{\sigma}{\mathcal{B}}^{2}+\epsilon}} $$

$$ \boldsymbol{y}^{(i)} \leftarrow \boldsymbol{\gamma} \odot \hat{\boldsymbol{x}}^{(i)}+\boldsymbol{\beta} $$

经过这样处理，就可以使得数据符合均值为、方差为的高斯分布。

下面看一下原文中批量归一化的算法步骤：

获取每次训练过程中的样本
就算小批量样本的均值、方差
归一化
拉伸和偏移

这里要着重介绍一下最后一步尺度变换(scale and shift)，前面3步已经对数据进行了归一化，为什么还需要拉伸和偏移呢？

因为经过前三步的计算使得数据被严格的限制为均值为0、方差为1的正态分布之下，这样虽然一定程度上解决了训练困难的问题，但是这样的严格限制网络的表达能力，通过加入和这两个参数可以使得数据分布的自由度更高，网络表达能力更强。另外，这两个参数和其他参数相同，通过不断的学习得出。

tensorflow中BN的使用

在tensorflow中可以直接调用批量归一化对数据进行处理，它的函数为，

tf.nn.batch_normalization(x, mean, variance, offset, scale, variance_epsilon, name=None)

来解释一下函数中参数的含义：

x：输入的数据，可以是卷积层的输出，也可以是全连接层的输出
mean：输出数据的均值
variance：输出数据的方差
offset：偏移，就是前面提到的beta
scale：缩放，前面提到的gamma
variance_epsilon：一个极小的值，避免分母为0

3.5 Dropout

前言

在前几讲里已经介绍了卷积神经网络中常用的一些单元，例如，

卷积层
池化层
填充
激活函数
批量归一化

本文会介绍最后一个卷积神经网络中常用的单元Dropout，可以称之为“丢弃法”，或者“随机失活”。它在2012年由Alex Krizhevsky、Geoffrey Hinton提出的那个大名鼎鼎的卷积神经网络模型AlexNet中首次提出并使用，Dropout的使用也是AlexNet与20世纪90年代提出的LeNet的最大不同之处。随后，Krizhevsky和Hinton在文章《Dropout: A Simple Way to Prevent Neural Networks from Over tting》又详细的介绍了介绍了Dropout的原理。发展至今，Dropout已经成为深度学习领域一个举足轻重的技术，它的价值主要体现在解决模型的过拟合问题，虽然它不是唯一的解决过拟合的手段，但它却是兼备轻量化和高效两点做的最好的一个手段。

“丢弃法”，从字面意思很好理解，就是丢弃网络中的一些东西。丢弃的是什么？神经元，有放回的随机丢弃一些神经元。

很多刚接触或者使用过Dropout的同学都会觉得“这有什么好讲的？这是一个非常简单的东西啊。”，如果仅仅从使用角度来讲，这的确非常简单。以目前主流的机器学习平台而言，tensorflow、mxnet、pytorch，均是传入一个概率值即可，一行代码即可完成。但是，我认为学习深度学习如果仅仅是为了会使用，那么真的没什么可以学习的，抽空把tensorflow教程看一下既可以称得上入门深度学习。如果剖开表象看一下Dropout的原理，会发现，它的理论基础是非常深的，从作者先后用《Improving neural networks by preventing co-adaptation of feature detectors》《Dropout: A Simple Way to Prevent Neural Networks from Over tting》等多篇文章来阐述这个算法就可以看出它的不可小觑的价值。

和往常先讲理论再讲用法不同，本文先介绍一下它在tensorflow中的用法，然后做一个了解后带着问题去介绍它的理论知识，本文主要包括如下几块内容，

tensorflow中Dropout的使用
优化与机器学习的区别
过拟合
Dropout理论知识

tensorflow中Dropout的使用

在tensorflow中Dropout的函数为，

tf.nn.dropout(x, keep_prob, noise_shape=None, seed=None, name=None)

函数中的参数分别是：

x：Dropout的输入，即为上一层网络的输出

keep_prob：和x尺寸相同的张量(多维向量)，它用于定义每个神经元的被保留的概率，假如keep_prob=0.8，那么它被保留的概率为0.8，换个角度说，它有20%的概率被丢弃。

noise_shape：表示随机生成的保存/删除标志的形状，默认值为None。

seed：一个用于创建随机种子的整数，默认值为None。

name：运算或操作的名称，可自行定义，默认值为None。

上述5个参数中x和keep_prob为必须参数，其他很少用到，所以不多介绍。x不难理解，就是上一层网络的输出。这里主要提示一下keep_prob，它是Dropout使用中最为重要的参数。

注意：keep_prob是网络中每个神经元被保留的概率，并非是神经网络中神经元被保留个数的概率。举个例子，加入有个3层神经网络，共100个神经元，定义keep_prob=0.6，那么并不是说要保留60个神经元而丢弃40个。而是每个神经元将会有60%的概率被保留，40%的概率被丢弃，所以最终剩余的神经元并不是确切的60个，可能多于60也可能少于60。

策略：深度学习是一门经验主义非常重的方向，Dropout的使用同样需要很多经验。一般情况下建议靠近输入层的把keep_prob设置大一些，就是靠近输入层经历多保留神经元。

优化与机器学习的区别

讲完Dropout的使用，话说回来，为什么要用Dropout？

提到这个问题，就不得不先做一下铺垫，先谈一下优化与机器学习的区别。

机器学习主要包括如下几块内容：

数据集
模型
损失函数
优化算法

其中优化算法直接决定着最终模型效果的好坏，因此，很多人都肆意的扩大优化算法的价值，认为“机器学习就是优化算法”。

我认为这是不严谨的说法机器学习与优化算法有这本质的区别。优化算法主要用于已知或未知数学模型的优化问题，它主要关注的是在既定模型上的误差，而不关注它的泛化误差。而机器学习则不同，它是在训练集上训练书模型，训练过程中与优化算法类似，考虑在训练集上的误差，但是它对比于优化算法还要多一步，要考虑在测试集上的泛化误差。

过拟合

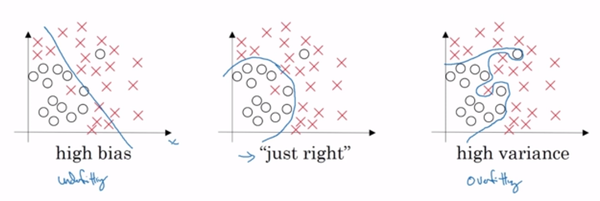
(图片截取自吴恩达《深度学习工程师》)

在训练集和测试集这两个数据集上的精确度就引出几种情况：

在训练集上效果不好，在测试集上效果也不好：欠拟合(上图中第一种情况)
在训练集上效果很好，在测试集上效果不好：过拟合(上图中第三种情况)

在实际项目中，这两种情况是非常常见的，显然，这并不是我们想要的，我们追求的是第三种情况：

在训练集和测试集上的效果都相对较好(上图中第二种情况)

但是，事与愿违，欠拟合和过拟合是机器学习中非常常见的现象，尤其是过拟合。

过拟合的形成原因主要包括如下几点：

训练数据集太少
参数过多
特征维度过高
模型过于复杂
噪声多

很多研究者把目光和精力都聚焦在解决过拟合这个问题上，目前用于解决过拟合问题的算法有很多，例如，

权重衰减
Early stopping
批量归一化(没错，就是前一讲讲的BN，它也带有一些正则化的功能)

在解决过拟合问题的算法中最为知名的词汇莫过于正则化。

提到正则化，很多同学会想到L1、L2正则化，其实它是一类方法的统称，并非仅限于L1、L2正则化，目前用于结果过拟合的正则化方法主要包括如下几种：

数据扩充
L1、L2正则化
Dropout

没错，Dropout也是正则化方法中的一种！铺垫这么多，终于引出本文的主角了。

数据扩充解决过拟合，这一点不难理解，因为数据缺少是引起过拟合的主要原因之一，由于数据的却是导致模型学习过程中不能学到全局特征，只能通过少量数据学习到一个类别的部分特征，通过数据的扩充能够让模型学习到全局特征，减少过拟合现象。

L1、L2正则化主要为损失函数添加一个L1或L2的正则化惩罚项，防止学习过程中过于偏向于某一个方向引起过拟合。

最后就轮到Dropout，下面来详细讲一下Dropout的原理。

Dropout

如何使用Dropout？

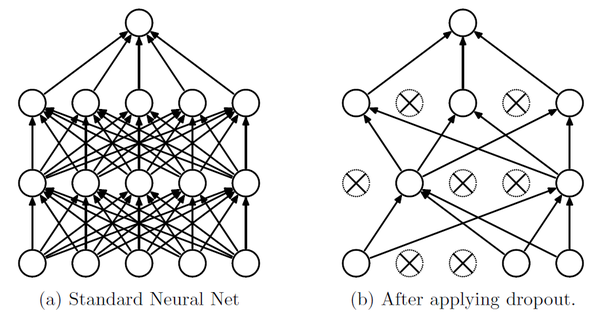
(图片来自于《Dropout: A Simple Way to Prevent Neural Networks from Over tting》)

上图中左图为一个标准的神经网络，右图是采用Dropout之后的神经网络，其中的区别一目了然，就是丢弃了一些神经元。

前面已经讲解了在tensorflow中如何使用Dropout，已经清楚，对于Dropout最为核心的就是保留概率或者丢弃概率，简述它的原理就是：遍历神经网络的每一层中每一个神经元，以一定概率丢弃或保留某个神经元。用数学语言描述如下，

假设某一个神经元的输入有4个，那么神经元的计算表达式为，

$$ h_{i}=\phi\left(x_{1} w_{1 i}+x_{2} w_{2 i}+x_{3} w_{3 i}+x_{4} w_{4 i}+b_{i}\right) $$

其中是输入，是权重，是偏差。

假设保留概率为 $p$ ，那么丢弃改为就为$1-p$，那么神经元 $h_i$ 就有 $1-p$ 的概率被丢弃，那么经过Dropout运算后的神经元为，

$$ h_{i}^{\prime}=\frac{\xi_{i}}{1-p} h_{i} $$

其中 $\xi_{i}$ 为0或者1，它为0或者1的概率分别为$1-p$ ，如果为0,则这个神经元被清零，临时被丢弃，一定要注意，是临时的丢弃，Dropout是有放回的采样。在一轮训练中前向或反向传播都会用丢弃后的神经网络，下一轮训练又会随机丢弃，用一个新的网络去训练。

编程实现Dropout其实只需要几行代码，下面结合代码来解释，会更容易理解，

def dropout(X, keep_prob):
    assert 0 < keep_prob < 1
    if keep_prob == 0:
        return np.zeros(X.shape)
    mask = np.random.uniform(0, 1, X.shape) < keep_prob
    return mask * X / keep_prob

输入参数为上一层的激活值和保留概率，

第3行：如果保留概率为0，也就是不保留的话，则全部元素都丢弃。

第5行：生成一个随机的掩码，掩码和输入X形状相同，每个位置非0即1，然后用这个掩码与X相乘，如果对应位置乘以0，则这个神经元被丢弃，反之保留。

Dropout为什么起作用？

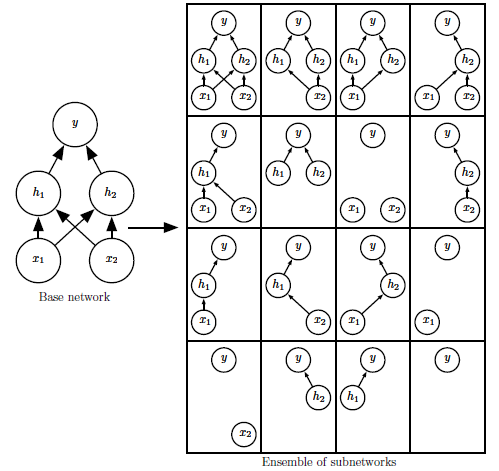
(图片来自《深度学习》)

这里不得不提一下Bagging集成集成学习方法，在Bagging集成学习方法中，预先会定义k的模型，然后采用k个训练集，然后分别训练k个模型，然后以各种方式去评价、选取最终学习的模型。

Dropout的训练过程中与Bagging集成学习方法类似，以上图为例，有一个三层神经网络(两个输入神经元、两个隐藏神经元、一个输出神经元)，从这个基础的网络中随机删除非输出神经元来构建一些子集。这样每一次训练就如同在这些子集中随机选择一个不同的网络模型进行训练，最后通过"投票"或者平均等策略而选择出一个最好的模型。

其实这个思想并不陌生，在传统机器学习中Adaboost、随机森林都是采用集成学习的思想，效果非常好。采用Dropout后的深度神经网络和这类思想也是类似的，这样能够结合不同网络模型的训练结果对最终学习的模型进行评价，能够综合多数，筛选掉少数，即便是某个网络模型出现了过拟合，最终经过综合也会过滤掉，效果自然会好很多。

需要说明一点的是，虽然采用Dropout和其他集成学习方法思想有异曲同工之处，但是也有一些细节的差异。在Bagging中所有模型都是独立的，但是在Dropout中所有模型是共享参数的，每个子模型会继承父网络的网络参数，这样可以有效的节省内存的占用。

需要注意的点

到这里，Dropout的内容就讲解完了，总结一些本文，需要有几点需要注意，

keep_prob是每个神经元被保留的概率
Dropout和L1、L2、数据扩充都属于正则化方法
Dropout的丢弃是有放回的

参考文献

Dropout: A Simple Way to Prevent Neural Networks from Over tting
Dropout as data augmentation
Improving Neural Networks with Dropout
Improving neural networks by preventing co-adaptation of feature detectors
《深度学习》

3.6 LeNet

个人主页>>

GitHub>>

前言

提起卷积神经网络，也许可以避开VGG、GoogleNet，甚至可以忽略AleNet，但是很难不提及LeNet。

LeNet是由2019年图灵奖获得者、深度学习三位顶级大牛之二的Yann LeCun、Yoshua Bengio于1998年提出(Gradient-based learning applied to document recognition)，它也被认为被认为是最早的卷积神经网络模型。但是，由于算力和数据集的限制，卷积神经网络提出之后一直都被传统目标识别算法(特征提取+分类器)所压制。终于在沉寂了14年之后的2012年，AlexNet在ImageNet挑战赛上一骑绝尘，使得卷积神经网络又一次成为了研究的热点。

近几年入门计算机视觉的同学大多数都是从AlexNet甚至更新的网络模型入手，了解比较多的就是R-CNN系列和YOLO系列，在很多知名的课程中对LeNet的介绍也是非常浅显或者没有介绍。虽然近几年卷积神经网络模型在LeNet的基础上加入了很多新的单元，在效果方面要明显优于LeNet，但是作为卷积神经网络的基础和源头，它的很多思想对后来的卷积神经网络模型具有很深的影响，因此，我认为了解一下LeNet还是非常有必要的。

本文首先介绍一下LeNet的网络模型，然后使用tensorflow来一步一步实现LeNet。

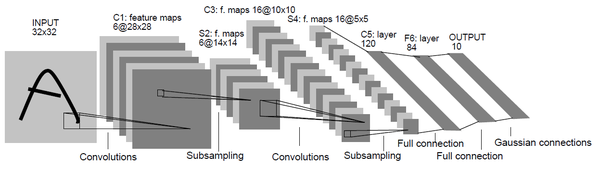
LeNet

上图就是LeNet的网络结构，LeNet又被称为LeNet-5，其之所以称为这个名称是由于原始的LeNet是一个5层的卷积神经网络，它主要包括两部分：

卷积层
全连接层

其中卷积层数为2，全连接层数为3。

这里需要注意一下，之前在介绍卷积、池化时特意提到，在网络层计数中池化和卷积往往是被算作一层的，虽然池化层也被称为"层"，但是它不是一个独立的运算，往往都是紧跟着卷积层使用，因此它不单独计数。在LeNet中也是这样，卷积层块其实是包括两个单元：卷积层与池化层。

在网络模型的搭建过程中，我们关注的除了网络层的结构，还需要关注一些超参数的设定，例如，卷积层中使用卷积核的大小、池化层的步幅等，下面就来介绍一下LeNet详细的网络结构和参数。

第一层：卷积层

卷积核大小为5*5，输入通道数根据图像而定，例如灰度图像为单通道，那么通道数为1，彩色图像为三通道，那么通道数为3。虽然输入通道数是一个变量，但是输出通道数是固定的为6。

池化层中窗口大小为2*2，步幅为2。

第二层：卷积层

卷积核大小为5*5，输入通道数即为上一层的输出通道数6，输出通道数为16。

池化层和第一层相同，窗口大小为2*2，步幅为2。

第三层：全连接层

全连接层顾名思义，就是把卷积层的输出进行展开，变为一个二维的矩阵(第一维是批量样本数，第二位是前一层输出的特征展开后的向量)，输入大小为上一层的输出16，输出大小为120。

第四层：全连接层

输入大小为120，输出大小为84。

第五层：全连接层

输入大小为84，输出大小为类别个数，这个根据不同任务而定，假如是二分类问题，那么输出就是2，对于手写字识别是一个10分类问题，那么输出就是10。

激活函数

前面文章中详细的介绍了激活函数的作用和使用方法，本文就不再赘述。激活函数有很多，例如Sigmoid、relu、双曲正切等，在LeNet中选取的激活函数为Sigmoid。

模型构建

如果已经了解一个卷积神经网络模型的结构，知道它有哪些层、每一层长什么样，那样借助目前成熟的机器学习平台是非常容易的，例如tensorflow、pytorch、mxnet、caffe这些都是高度集成的深度学习框架，虽然在强化学习、图神经网络中表现一般，但是在卷积神经网络方面还是很不错的。

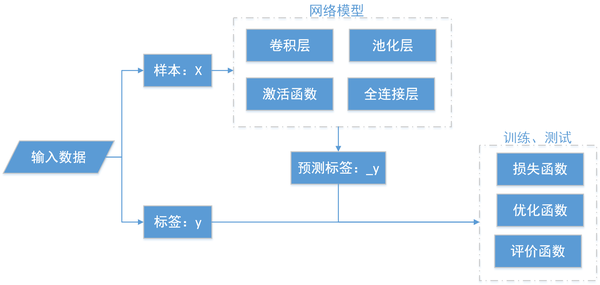
我绘制了模型构建的过程，详细的可以看一下上图，很多刚入门的同学会把tensorflow使用、网络搭建看成已经非常困难的事情，其实理清楚之后发现并没有那么复杂，它主要包括如下几个部分：

数据输入
网络模型
训练预测

其中，重点之处就在于网络模型的搭建，需要逐层的去搭建一个卷积神经网络，复杂程度因不同的模型而异。训练测试过程相对简单一些，可以通过交叉熵、均方差等构建损失函数，然后使用深度学习框架自带的优化函数进行优化即可，代码量非常少。

LeNet、AlexNet、VGG、ResNet等，各种卷积神经网络模型主要的区别之处就在于网络模型，但是网络搭建的过程是相同的，均是通过上述流程进行搭建，因此，本文单独用一块内容介绍模型搭建的过程，后续内容不再介绍网络模型的搭建，会直接使用tensorflow进行编程实践。

编程实践

首先需要说明一下，后续的内容中涉及网络模型搭建的均会选择tensorflow进行编写。虽然近几年pytorch的势头非常迅猛，关于tensorflow的批评之声不绝于耳，但是我一向认为，灵活性和易用性总是成反比的，tensorflow虽然相对复杂，但是它的灵活性非常强，而且支持强大的可视化tensorboard，虽然pytorch也可以借助tensorboard实现可视化，但是这样让我觉得有一些"不伦不类"的感觉，我更加倾向于一体化的框架。此外，有很多同学认为Gluon、keras非常好用，的确，这些在tensorflow、mxnet之上进一步封装的高级深度学习框架非常易用，很多参数甚至不需要开发者去定义，但是正是因为这样，它们已经强行的预先定义在框架里了，可想而知，它的灵活性是非常差的。因此，综合灵活性、一体化、丰富性等方面的考虑，本系列会采用tensorflow进行编程实践。

其次，需要说明的是本系列重点关注的是网络模型，因此，关于数据方面会采用MNIST进行实践。MNIST是一个成熟的手写字数据集，它提供了易用的接口，方便读取和处理。

在使用tensorflow接口读取MNIST时，如果本地有数据，它会从本地加载，否则它会从官网下载数据，如果由于代理或者网速限制的原因自动下载数据失败，可以手动从官网下载数据放在MNIST目录下，数据包括4个文件，分别是：

train-images-idx3-ubyte.gz
train-labels-idx1-ubyte.gz
t10k-images-idx3-ubyte.gz
t10k-labels-idx1-ubyte.gz

它们分别是训练数据集和标签，测试数据集和标签。

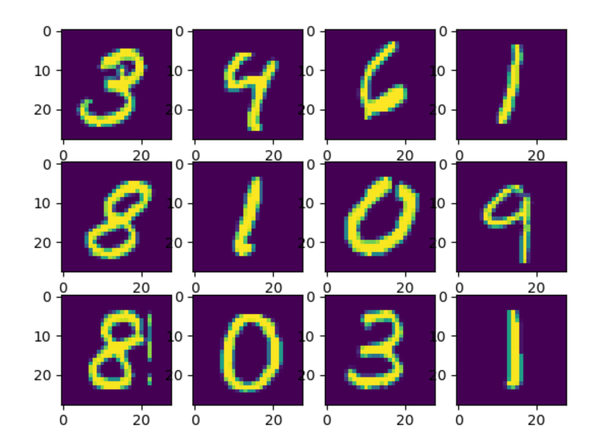
可能会有人有疑问，手写体识别不是图像吗？为什么是gz的压缩包？因为作者对手写体进行了序列化处理，方便读取，数据原本是衣服单通道28*28的灰度图像，处理后是784的向量，我们可以通过一段代码对它可视化一下，

from matplotlib import pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("MNIST", one_hot=True)
for i in range(12):
    plt.subplot(3, 4, i+1)
    img = mnist.train.images[i + 1]
    img = img.reshape(28, 28)
    plt.imshow(img)
plt.show()

通过读取训练集中的12副图像，然后把它修改成28*28的图像，显示之后会发现和我们常见的图像一样，

下面开始一步一步进行搭建网络LeNet，由前面介绍的模型构建过程可以知道，其中最为核心的就是搭建模型的网络架构，所以，首先先搭建网络模型，

$$ y=wx+b $$

卷积的运算是符合上述公式的，因此，首先构造第一层网络，输入为批量784维的向量，需要首先把它转化为28*28的图像，然后初始化卷积核，进行卷积、激活、池化运算，

X = tf.reshape(X, [-1, 28, 28, 1])
w_1 = tf.get_variable("weights", shape=[5, 5, 1, 6])
b_1 = tf.get_variable("bias", shape=[6])
conv_1 = tf.nn.conv2d(X, w_1, strides=[1, 1, 1, 1], padding="SAME")
act_1 = tf.sigmoid(tf.nn.bias_add(conv_1, b_1))
max_pool_1 = tf.nn.max_pool(act_1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")

然后构建第二层网络，

w_2 = tf.get_variable("weights", shape=[5, 5, 6, 16])
b_2 = tf.get_variable("bias", shape=[16])
conv_2 = tf.nn.conv2d(max_pool_1, w_2, strides=[1, 1, 1, 1], padding="SAME")
act_2 = tf.nn.sigmoid(tf.nn.bias_add(conv_2, b_2))
max_pool_2 = tf.nn.max_pool(act_2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")

到这里，卷积层就搭建完了，下面就开始搭建全连接层。

首先需要把卷积层的输出进行展开成向量，

flatten = tf.reshape(max_pool_2, shape=[-1, 2 * 2 * 16])

然后紧接着是3个全连接层，

# 全连接层1
with tf.variable_scope("fc_1") as scope:
    w_fc_1 = tf.get_variable("weight", shape=[2 * 2 * 16, 120])
    b_fc_1 = tf.get_variable("bias", shape=[120], trainable=True)
fc_1 = tf.nn.xw_plus_b(flatten, w_fc_1, b_fc_1)
act_fc_1 = tf.nn.sigmoid(fc_1)

# 全连接层2
with tf.variable_scope("fc_2") as scope:
    w_fc_2 = tf.get_variable("weight", shape=[120, 84])
    b_fc_2 = tf.get_variable("bias", shape=[84], trainable=True)
fc_2 = tf.nn.xw_plus_b(act_fc_1, w_fc_2, b_fc_2)
act_fc_2 = tf.nn.sigmoid(fc_2)

# 全连接层3
with tf.variable_scope("fc_3") as scope:
    w_fc_3 = tf.get_variable("weight", shape=[84, 10])
    b_fc_3 = tf.get_variable("bias", shape=[10], trainable=True)
fc_3 = tf.nn.xw_plus_b(act_fc_2, w_fc_3, b_fc_3)

这样就把整个网络模型搭完成了，输入是批量图像X，输出是预测的图像，输出是一个10维向量，每一维的含义是当前数字的概率，选择概率最大的位置，就是图像对应的数字。

完成了网络模型的搭建，它能够将输入图像转化成预测标签进行输出，接下来要做的就是训练和测试部分。

def train():
    # 1. 输入数据的占位符
    x = tf.placeholder(tf.float32, [None, 784])
    y = tf.placeholder(tf.float32, [BATCH_SIZE, 10])
    
    # 2. 初始化LeNet模型，构造输出标签y_
    le = LeNet()
    y_ = le.create(x)
    
    # 3. 损失函数，使用交叉熵作为损失函数
    loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=y_, labels=y))
    
    # 4. 优化函数，首先声明I个优化函数，然后调用minimize去最小化损失函数
    optimizer = tf.train.AdamOptimizer()
    train_op = optimizer.minimize(loss)
    
    # 5. summary用于数据保存，用于tensorboard可视化
    tf.summary.scalar("loss", loss)
    merged = tf.summary.merge_all()
    writer = tf.summary.FileWriter("logs")
    
    # 6. 构造验证函数，如果对应位置相同则返回true，否则返回false
    correct_pred = tf.equal(tf.argmax(y_, 1), tf.argmax(y, 1))
    
    # 7. 通过tf.cast把true、false布尔型的值转化为数值型，分别转化为1和0，然后相加就是判断正确的数量
    accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

    # 8. 初始化一个saver，用于后面保存训练好的模型
    saver = tf.train.Saver()
    with tf.Session() as sess:
        # 9. 初始化变量
        sess.run((tf.global_variables_initializer()))
        writer.add_graph(sess.graph)
        i = 0
        for epoch in range(5):
            for step in range(1000):
                # 10. feed_dict把数据传递给前面定义的占位符x、y
                batch_xs, batch_ys = mnist.train.next_batch(BATCH_SIZE)
                summary, loss_value, _ = sess.run(([merged, loss, train_op]),
                                                  feed_dict={x: batch_xs,
                                                             y: batch_ys})
                print("epoch : {}----loss : {}".format(epoch, loss_value))
                # 11. 记录数据点
                writer.add_summary(summary, i)
                i += 1
                
        # 验证准确率
        test_acc = 0
        test_count = 0
        for _ in range(10):
            batch_xs, batch_ys = mnist.test.next_batch(BATCH_SIZE)
            acc = sess.run(accuracy, feed_dict={x: batch_xs, y: batch_ys})
            test_acc += acc
            test_count += 1
        print("accuracy : {}".format(test_acc / test_count))
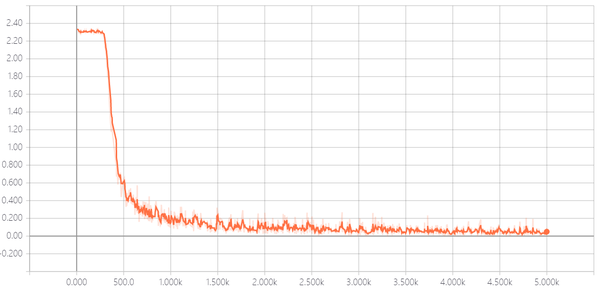
        saver.save(sess, os.path.join("temp", "mode.ckpt"))

上述就是训练部分的完整代码，在代码中已经详细的注释了每个部分的功能，分别包含数据记录、损失函数、优化函数、验证函数、训练过程等，然后运行代码可以看到效果，

...
epoch : 4----loss : 0.07602085173130035
epoch : 4----loss : 0.05565792694687843
epoch : 4----loss : 0.08458487689495087
epoch : 4----loss : 0.012194767594337463
epoch : 4----loss : 0.026294417679309845
epoch : 4----loss : 0.04952147603034973
accuracy : 0.9953125

准确率为99.5%，可以看得出，在效果方面，LeNet在某些任务方面并不比深度卷积神经网络差。

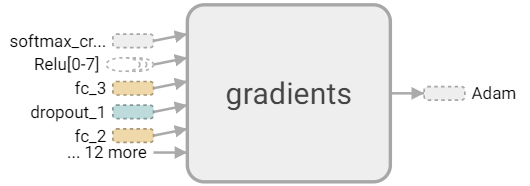
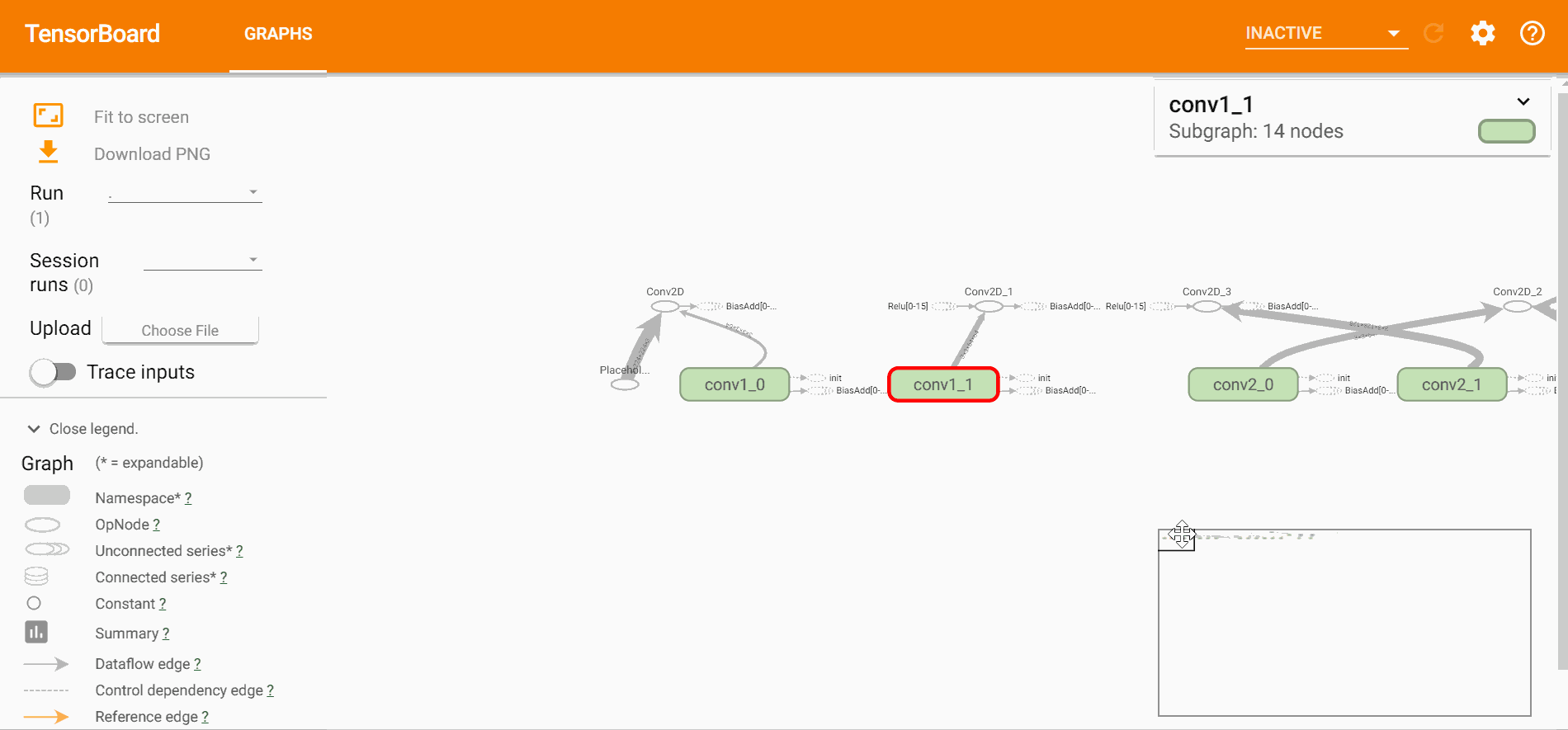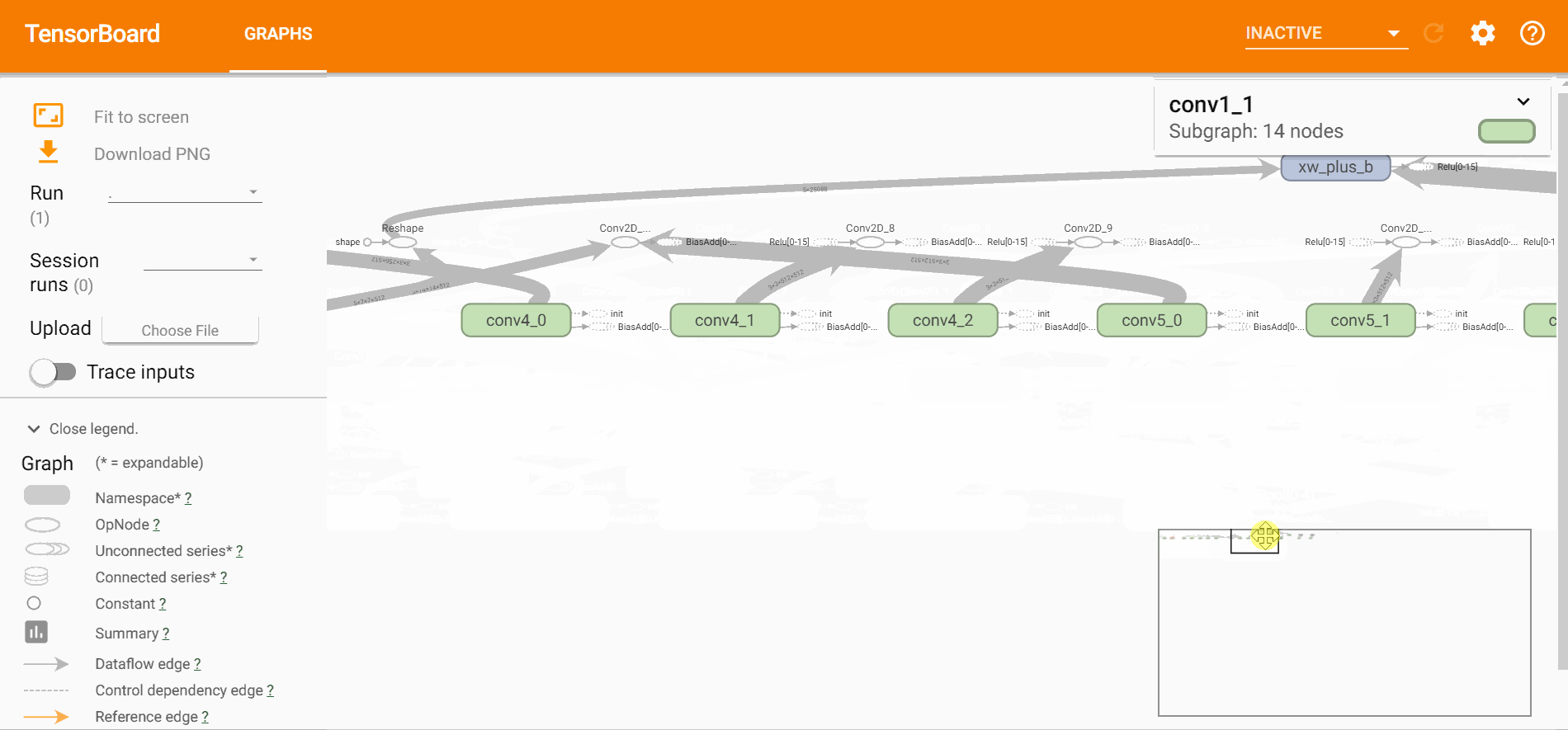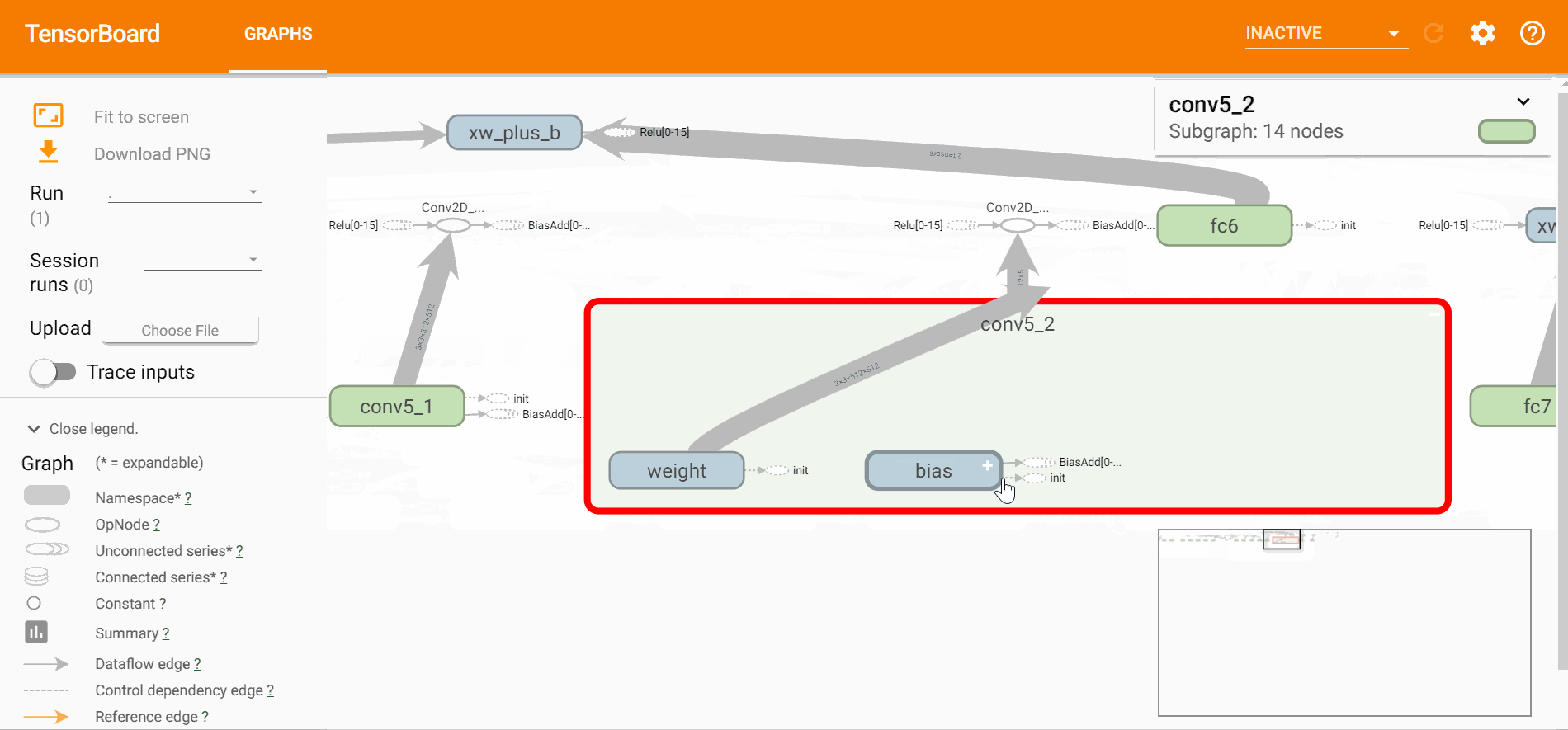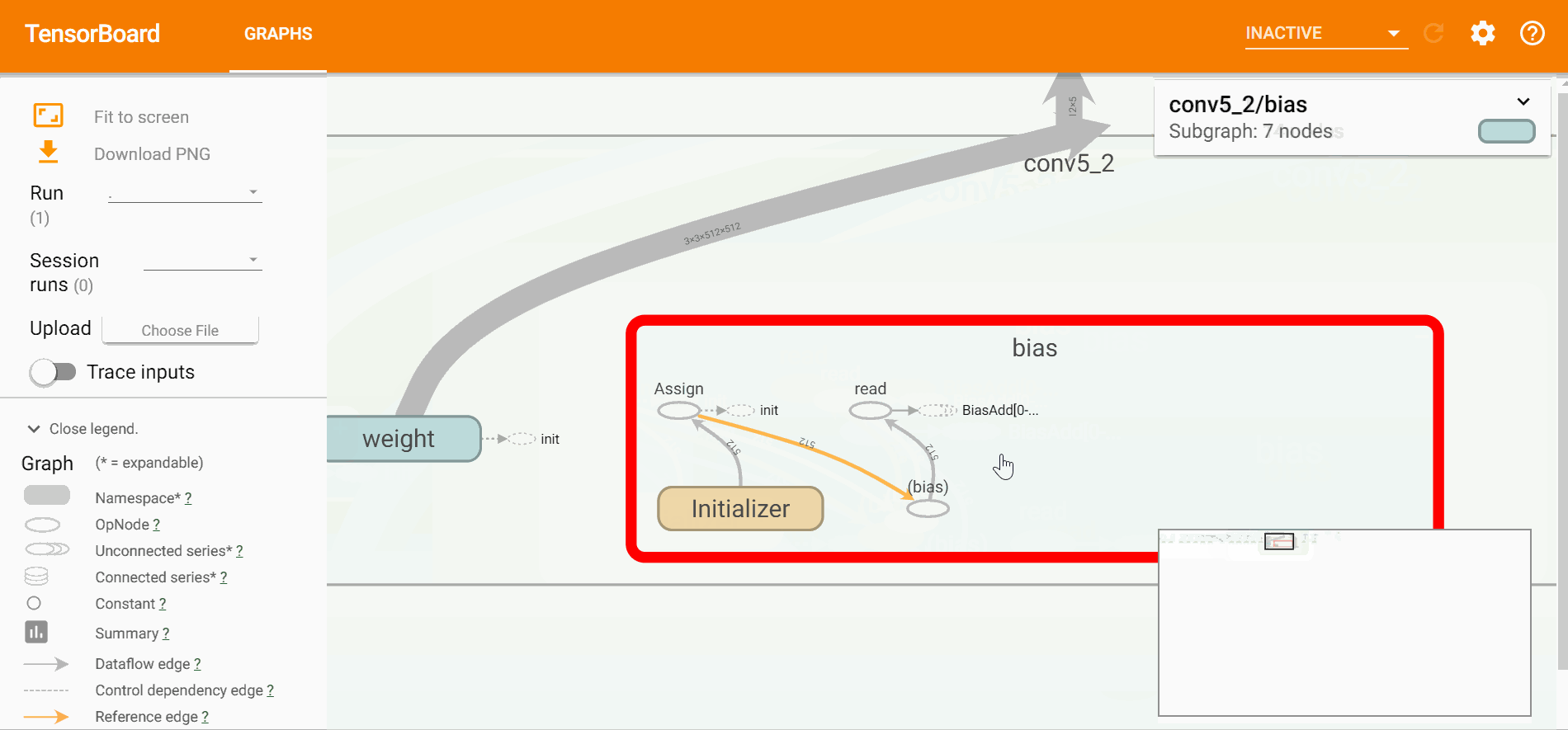
打开tensorboard可以直观的看到网络的结构、训练的过程以及训练中数据的变换，

$ tensorboard --logdir=logs

tensorboard直观效果如下，

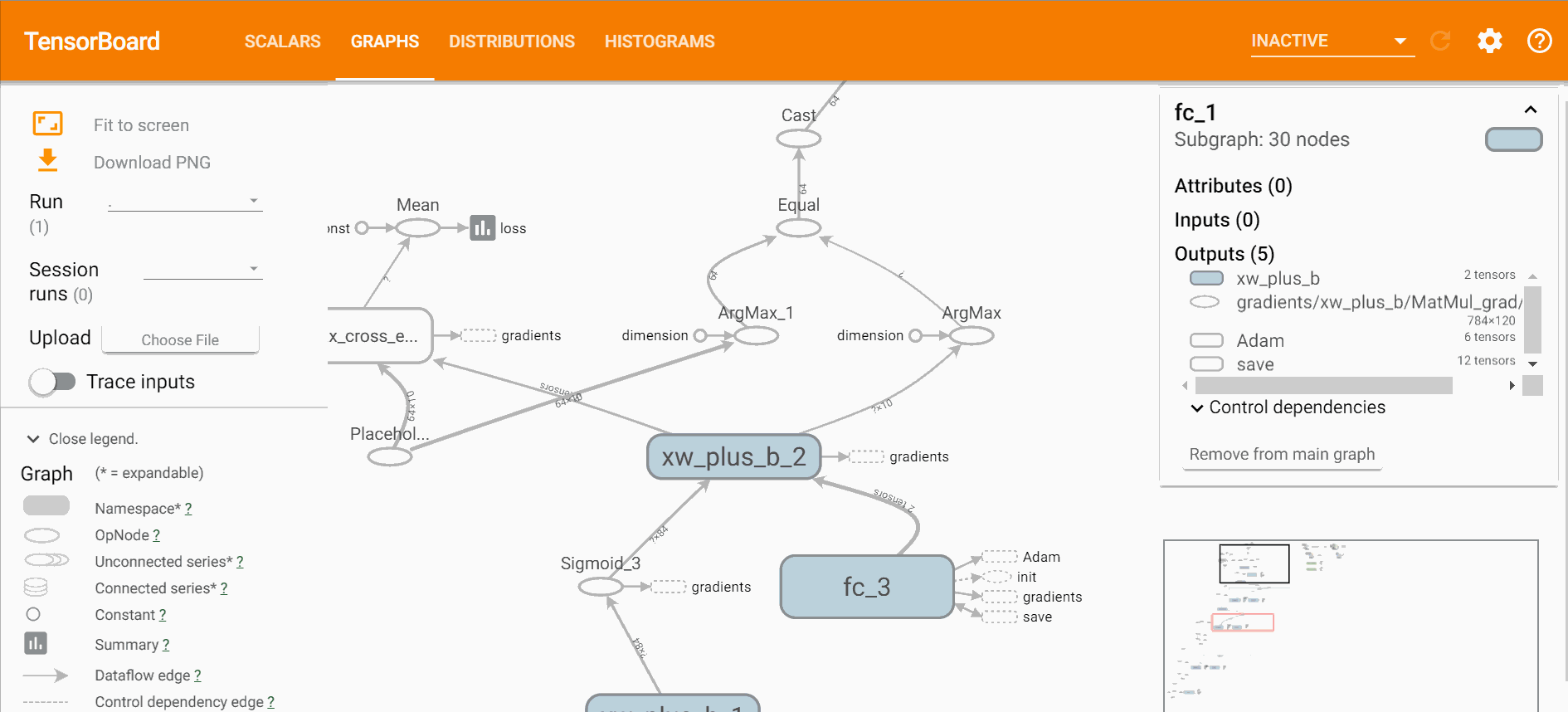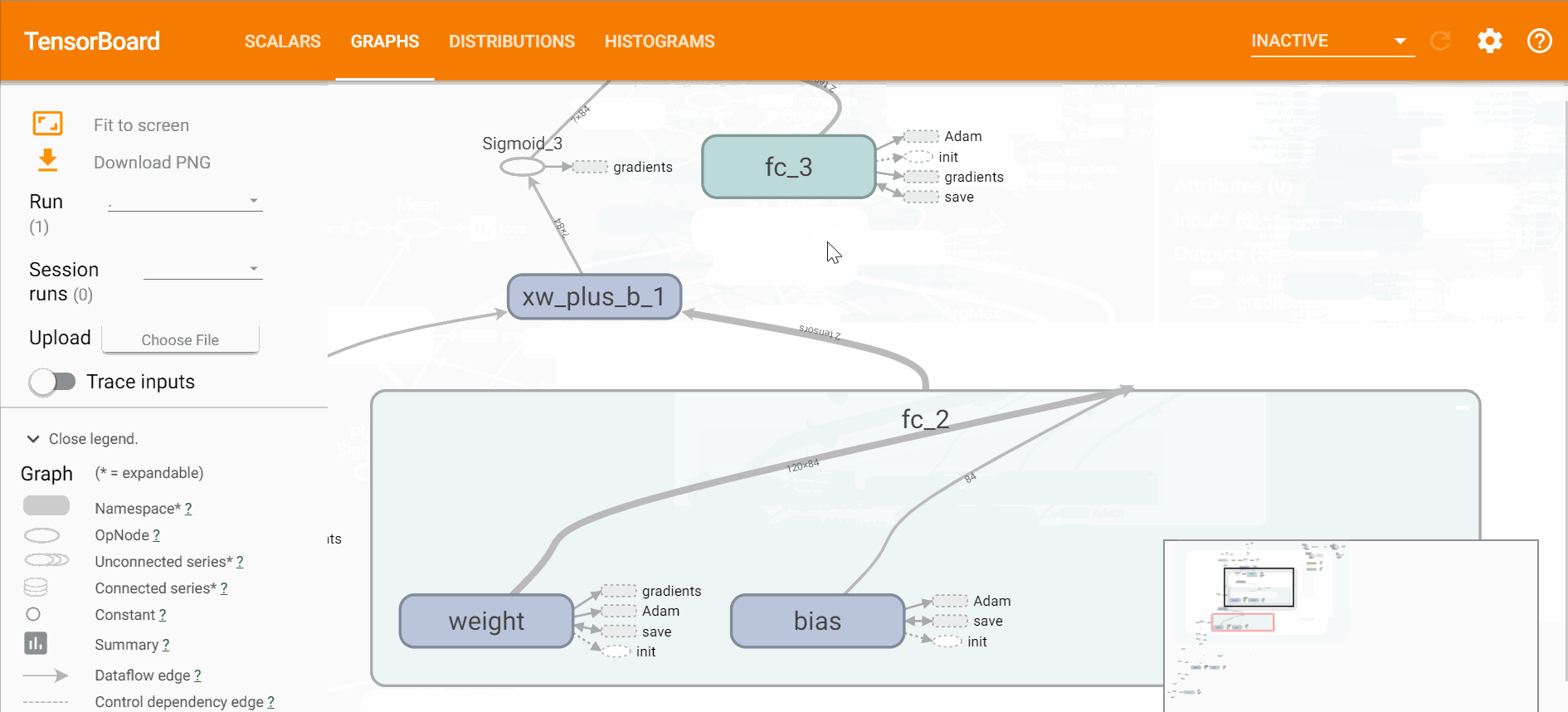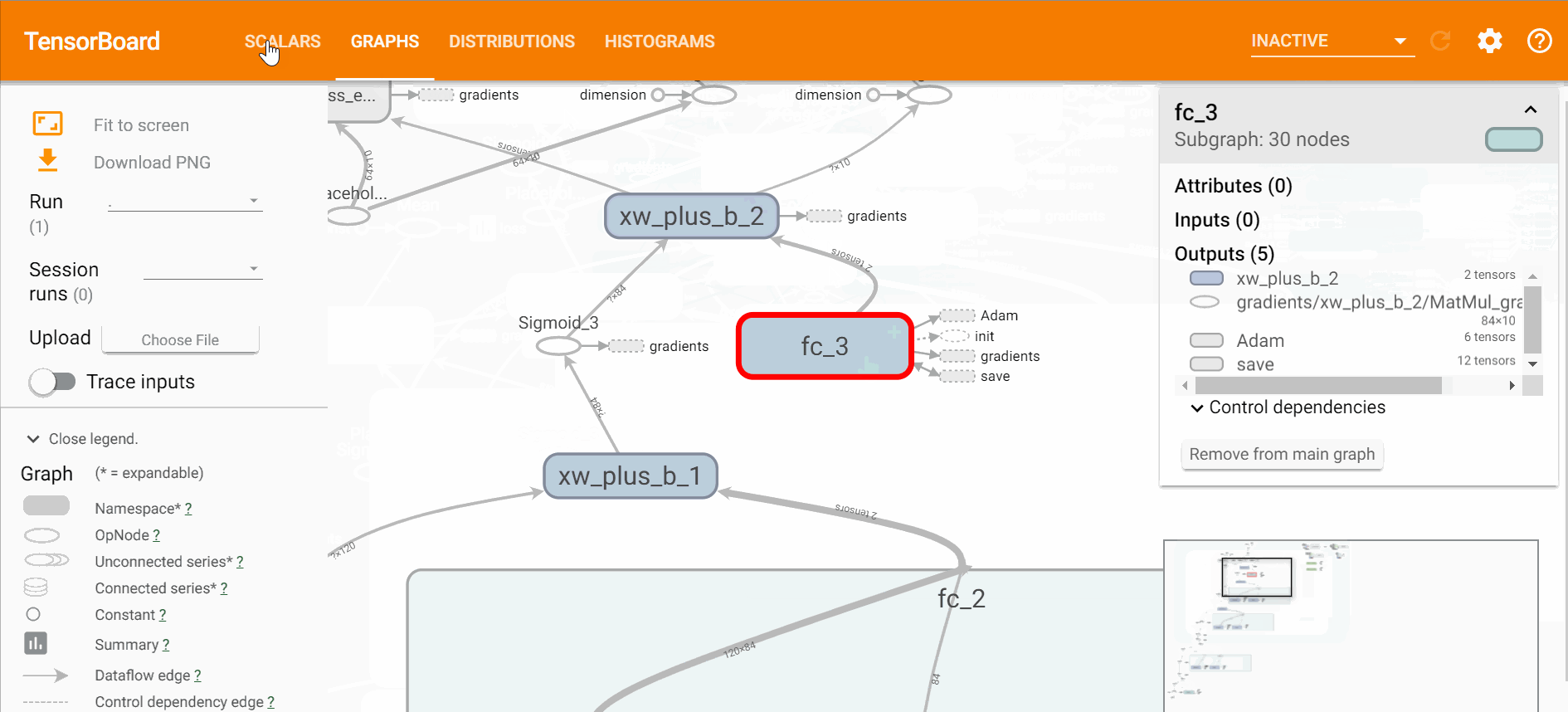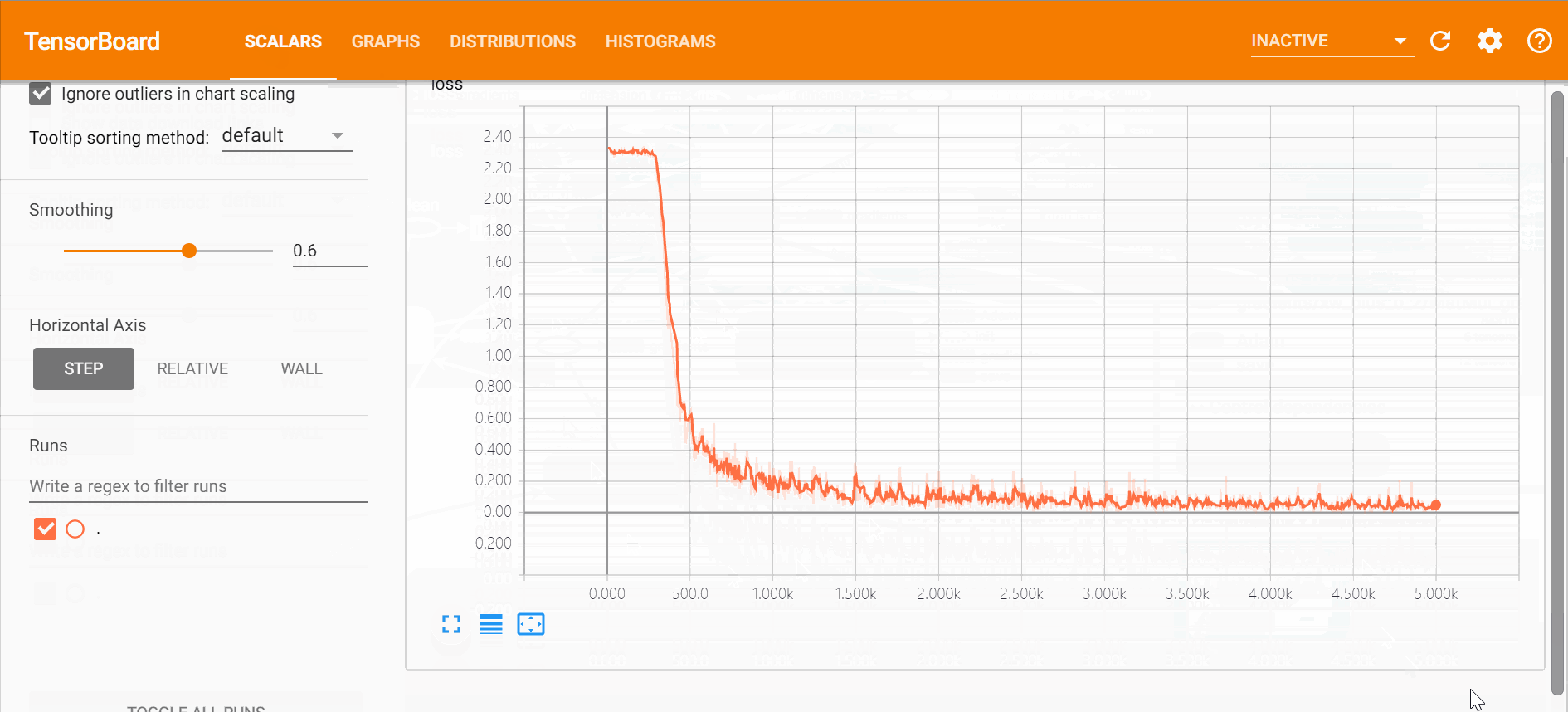
通过损失函数的变化过程可以看出，训练过程在2000步左右基本达到了最优解，

3.7 AlexNet

前言

前文详细介绍了卷积神经网络的开山之作LeNet，虽然近几年卷积神经网络非常热门，但是在LeNet出现后的十几年里，在目标识别领域卷积神经网络一直被传统目标识别算法(特征提取+分类器)所压制，直到2012年AlexNet(ImageNet Classification with Deep Convolutional Neural Networks)在ImageNet挑战赛一举夺魁，使得卷积神经网络再次引起人们的重视，并因此而一发不可收拾，卷积神经网络的研究如雨后春笋一般不断涌现，推陈出新。

AlexNet是以它的第一作者Alex Krizhevsky而命名，这篇文章中也有深度学习领域三位大牛之一的Geoffrey Hinton的身影。AlexNet之所以这么有名气，不仅仅是因为获取比赛冠军这么简单。这么多年，目标识别、目标跟踪相关的比赛层出不穷，获得冠军的团队也变得非常庞大，但是反观一下能够像 AlexNet影响力这么大的，却是寥寥可数。

AlexNet相比于上一代的LeNet它首先在数据集上做了很多工作，

第一点：数据集

我们都知道，限制深度学习的两大因素分别输算力和数据集，AlexNet引入了数据增广技术，对图像进行颜色变换、裁剪、翻转等操作。

第二点：激活函数

在激活函数方面它采用ReLU函数代替Sigmoid函数，前面我用一篇文章详细的介绍了不同激活函数的优缺点，如果看过的同学应该清楚，ReLU激活函数不仅在计算方面比Sigmoid更加简单，而且可以克服Sigmoid函数在接近0和1时难以训练的问题。

第三点：Dropout

这也是AlexNet相对于LeNet比较大一点不同之处，AlexNet引入了Dropout用于解决模型训练过程中容易出现过拟合的问题，此后作者还发表几篇文章详细的介绍Dropout算法，它的引入使得卷积神经网络效果大大提升，直到如今Dropout在模型训练过程中依然被广泛使用。

第四点：模型结构

卷积神经网络的每次迭代，模型架构都会发生非常大的变化，卷积核大小、网络层数、跳跃连接等等，这也是不同卷积神经网络模型之间的区别最明显的一点，由于网络模型比较庞大，一言半语无法描述完整，下面我就来详细介绍一下AlexNet的网络模型。

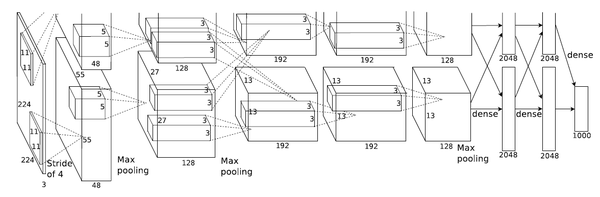
AlexNet

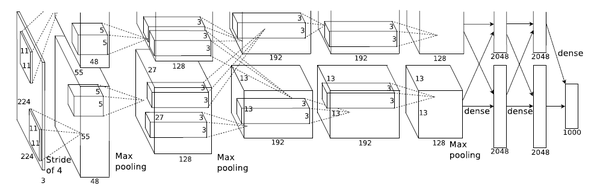
如果读过前面一片文章应该了解，LeNet是一个5层的卷积神经网络模型，它有两个卷积层和3个全连接层。对比而言，AlexNet是一个8层的卷积升级网络模型，它有5个卷积层和3个全连接层。

我们在搭建一个网络模型的过程中，重点应该关注如下几点：

卷积核大小
输入输出通道数
步长
激活函数

关于AlexNet中使用的激活函数前面已经介绍过，它使用的是ReLU激活函数，它5层卷积层除了第一层卷积核为11*11、第二次为5*5之外，其余三层均为3*3，下面就详细介绍一下AlexNet的模型结构，

第一层：卷积层

卷积核大小11*11，输入通道数根据输入图像而定，输出通道数为96，步长为4。

池化层窗口大小为3*3，步长为2。

第二层：卷积层

卷积核大小5*5，输入通道数为96，输出通道数为256，步长为2。

池化层窗口大小为3*3，步长为2。

第三层：卷积层

卷积核大小3*3，输入通道数为256，输出通道数为384，步长为1。

第四层：卷积层

卷积核大小3*3，输入通道数为384，输出通道数为384，步长为1。

第五层：卷积层

卷积核大小3*3，输入通道数为384，输出通道数为256，步长为1。

池化层窗口大小为3*3，步长为2。

第六层：全连接层

输入大小为上一层的输出，输出大小为4096。

Dropout概率为0.5。

第七层：全连接层

输入大小为4096，输出大小为4096。

Dropout概率为0.5。

第八层：全连接层

输入大小为4096，输出大小为分类数。

**注意：**需要注意一点，5个卷积层中前2个卷积层后面都会紧跟一个池化层，而第3、4层卷积层后面没有池化层，而是连续3、4、5层三个卷积层后才加入一个池化层。

编程实践

在动手实践LeNet文章中，我介绍了网络搭建的过程，这种方式同样适用于除LeNet之外的其他模型的搭建，我们需要首先完成网络模型的搭建，然后再编写训练、验证函数部分。

在前面一篇文章为了让大家更加容易理解tensorflow的使用，更加清晰的看到网络搭建的过程，因此逐行编码进行模型搭建。但是，我们会发现，同类型的网络层之间很多参数是相同的，例如卷积核大小、输出通道数、变量作用于的名称，我们逐行搭建会有很多代码冗余，我们完全可以把这些通用参数作为传入参数提炼出来。因此，本文编程实践中会侧重于代码规范，提高代码的可读性。

编程实践中主要根据tensorflow接口的不同之处把网络架构分为如下4个模块：

卷积层
池化层
全连接层
Dropout

卷积层

针对卷积层，我们把输入、卷积核大小、输入通道数、步长、变量作用域作为入参，我们使用tensorflow时会发现，我们同样需要知道输入数据的通道数，关于这个变量，我们可以通过获取输入数据的尺寸获得，

def conv_layer(self, X, ksize, out_filters, stride, name):
    in_filters = int(X.get_shape()[-1])
    with tf.variable_scope(name) as scope:
        weight = tf.get_variable("weight", [ksize, ksize, in_filters, out_filters])
        bias = tf.get_variable("bias", [out_filters])
    conv = tf.nn.conv2d(X, weight, strides=[1, stride, stride, 1], padding="SAME")
    activation = tf.nn.relu(tf.nn.bias_add(conv, bias))
    return activation

上面，我们经过获取权重、偏差，卷积运算，激活函数3个部分完成了卷积模块的实现。AlexNet有5个卷积层，不同层之间的主要区别就体现在conv_layer的入参上面，因此我们只需要修改函数的入参就可以完成不同卷积层的搭建。

池化层

def pool_layer(self, X, ksize, stride):
    return tf.nn.max_pool(X, ksize=[1, ksize, ksize, 1], strides=[1, stride, stride, 1], padding="SAME")

全连接层

def full_connect_layer(self, X, out_filters, name):
    in_filters = X.get_shape()[-1]
    with tf.variable_scope(name) as scope:
        w_fc = tf.get_variable("weight", shape=[in_filters, out_filters])
        b_fc = tf.get_variable("bias", shape=[out_filters], trainable=True)
    fc = tf.nn.xw_plus_b(X, w_fc, b_fc)
    return tf.nn.relu(fc)

Dropout

def dropout(self, X, keep_prob):
    return tf.nn.dropout(X, keep_prob)

到这里，我们就完成了卷积层、池化层、全连接层、Dropout四个模块的编写，下面我们只需要把不同模块按照AlexNet的模型累加在一起即可，

模型

def create(self, X):
    X = tf.reshape(X, [-1, 28, 28, 1])
    conv_layer1 = self.conv_layer(X, 11, 96, 4, "Layer1")
    pool_layer1 = self.pool_layer(conv_layer1, 3, 2)

    conv_layer2 = self.conv_layer(pool_layer1, 5, 256, 2, "Layer2")
    pool_layer2 = self.pool_layer(conv_layer2, 3, 2)

    conv_layer3 = self.conv_layer(pool_layer2, 3, 384, 1, "Layer3")
    conv_layer4 = self.conv_layer(conv_layer3, 3, 384, 1, "Layer4")
    conv_layer5 = self.conv_layer(conv_layer4, 3, 256, 1, "Layer5")
    pool_layer = self.pool_layer(conv_layer5, 3, 2)
    _, x, y, z = pool_layer.get_shape()
    full_connect_size = x * y * z
    flatten = tf.reshape(pool_layer, [-1, full_connect_size])
    fc_1 = self.full_connect_layer(flatten, 4096, "fc_1")
    drop1 = self.dropout(fc_1, self.keep_prob)
    fc_2 = self.full_connect_layer(drop1, 4096, "fc_2")
    drop2 = self.dropout(fc_2, self.keep_prob)
    fc_3 = self.full_connect_layer(drop2, self.num_classes, "fc_3")
    return fc_3

返回结果是一个1*m维的向量，其中m是类别数，以本文使用的MNIST为例，输入是一个1*10的详细，每一个数字对应于索引数字的概率值。

上述就是完整模型的搭建过程，下面我们就需要把输入传入模型，然后获取预测输出，进而构建误差函数进行训练模型。

训练验证

训练验证部分入参有3个，分别是，

输入数据
标签
预测值

其中输入数据和标签为占位符，会在图启动运算时传入真实数据，预测值为模型的输出，

def train_val(X, y, y_):
    loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=y_))
    optimizer = tf.train.AdamOptimizer(learning_rate=LR)
    train_op = optimizer.minimize(loss)
    tf.summary.scalar("loss", loss)

    correct_pred = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
    accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
    merged = tf.summary.merge_all()
    writer = tf.summary.FileWriter("logs")
    saver = tf.train.Saver()

    with tf.Session() as sess:
        sess.run(tf.global_variables_initializer())
        writer.add_graph(sess.graph)
        i = 0
        for epoch in range(EPOCHS):
            for step in range(MAX_STEPS):
                batch_xs, batch_ys = mnist.train.next_batch(BATCH_SIZE)
                summary, loss_val, _ = sess.run([merged, loss, train_op],
                                                feed_dict={X: batch_xs, y: batch_ys})
                print("epoch : {}----loss : {}".format(epoch, loss_val))
                writer.add_summary(summary, i)
                i += 1
        saver.save(sess, os.path.join("temp", "mode.ckpt"))

        test_acc = 0
        test_count = 0
        for _ in range(10):
            batch_xs, batch_ys = mnist.test.next_batch(BATCH_SIZE)
            acc = sess.run(accuracy, feed_dict={X: batch_xs, y: batch_ys})
            test_acc += acc
            test_count += 1
        print("accuracy : {}".format(test_acc / test_count))

上述就是AlexNet模型搭建和训练过程。

注意：同一个模型在不同的数据集上表现会存在很大差异，例如LeNet是在MNIST的基础上进行搭建和验证的，因此卷积核、步长等这些超参数都已经进行了精心的调节，因此只需要按照模型搭建完成即可得到99%以上的准确率。而AlexNet是在ImageNet的图像上进行调优的，ImageNet的图像相对于MNIST28*28的图像要大很多，因此卷积核、步长都要大很多，但是这样对于图像较小的MNIST来说就相对较大，很难提取细节特征，因此如果用默认的结构效果甚至比不上20年轻的LeNet。这也是为什么深度学习模型可复制性差的原因，尽管是两个非常类似的任务，同一个模型在两个任务上表现得效果也会存在很大的差异，这需要工程时对其进行反复的调节、优化。

3.8 VGG

前言

2014年对于计算机视觉领域是一个丰收的一年，在这一年的ImageNet图像识别挑战赛(ILSVRC,ImageNet Large Scale Visual Recognition Challenge)中出现了两个经典、响至深的卷积神经网络模型，其中第一名是GoogLeNet、第二名是VGG，都可以称得上是深度计算机视觉发展过程中的经典之作。

虽然在名次上GoogLeNet盖过了VGG，但是在可迁移性方面GoogLeNet对比于VGG却有很大的差距，而且在模型构建思想方面对比于它之前的AlexNet、LeNet做出了很大的改进，因此，VGG后来常作为后续卷积神经网络模型的基础模块，用于特征提取。直到5年后的今天，依然可以在很多新颖的CNN模型中可以见到VGG的身影，本文就来详细介绍一下这个经典的卷积神经网络模型。

VGG模型

VGG(VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION)，是由牛津大学的研究者提出，它的名称也是以作者所在实验室而命名(Visual Geometry Group)。

前一篇文章介绍了经典的AlexNet，虽然它在识别效果方面非常令人惊艳，但是这些都是建立在对超参数进行大量的调整的基础上，而它并没有提出一种明确的模型设计规则以便指导后续的新网络模型设计，这也限制了它的迁移能力。因此，虽然它很知名，但是在近几年的模型基础框架却很少出现AlexNet的身影，反观VGG则成为了很多新模型基础框架的必选项之一，这也是它相对于AlexNet的优势之一：VGG提出用基础块代替网络层的思想，这使得它在构建深度网络模型时可以重复使用这些基础块。

正如前面所说，VGG使用了块代替层的思想，具体的来说，它提出了构建基础的卷积块和全连接块来替代卷积层和全连接层，而这里的块是由多个输出通道相同的层组成。

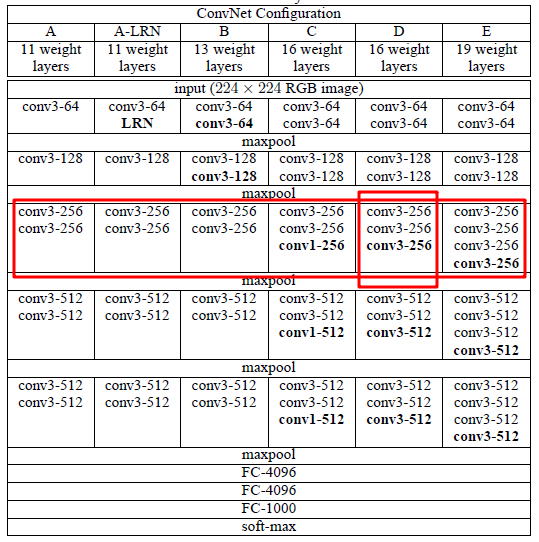
VGG和AlexNet指代单一的模型不同，VGG其实包含多个不同的模型，从上图可以看出，它主要包括下列模型，

VGG-11
VGG-13
VGG-16
VGG-19

其中，后面的数字11、13、16、19是网络层数。

从图中可以看出，VGG的特点是每个卷积块(由1个或多个卷积层组成)后面跟随一个最大池化层，整体架构和AlexNet非常类似，主要区别就是把层替换成了块。

从图中红框标记可以看出，每个卷积块中输出通道数相同，另外从横向维度来看，不同模型在相同卷积块中输出通道也相同。

下面就以比较常用的VGG-16这个模型为例来介绍一下VGG的模型架构。

VGG-16是由5个卷积块和3个全连接层共8部分组成(回想一下，AlexNet也是由8个部分组成，只不过AlexNet是由5个卷积层和3个全连接层组成)，下面详细介绍每一个部门的详细情况。

注意：前两篇文章我们在搭建LeNet和AlexNet时会发现，不同层的卷积核、步长均有差别，这也是迁移过程中比较困难的一点，而在VGG中就没有这样的困扰，VGG卷积块中统一采用的是3*3的卷积核，卷积层的步长均为1，而在池化层窗口大小统一采用2*2，步长为2。因为每个卷积层、池化层窗口大小、步长都是确定的，因此要搭建VGG我们只需要关注每一层输入输出的通道数即可。

卷积块1

包含2个卷积层，输入是224*224*3的图像，输入通道数为3，输出通道数为64。

卷积块2

包含2个卷积层，输入是上一个卷积块的输出，输入通道数为64，输出通道数为128。

卷积块3

包含3个卷积层，输入是上一个卷积块的输出，输入通道数为128，输出通道数为256。

卷积块4

包含3个卷积层，输入是上一个卷积块的输出，输入通道数为256，输出通道数为512。

卷积块5

包含3个卷积层，输入是上一个卷积块的输出，输入通道数为512，输出通道数为512。

全连接层1

输入为上一层的输出，输入通道数为前一卷积块输出reshape成一维的长度,输出通道数为4096。

全连接层2

输入为上一层的输出，输入通道数为4096,输出通道数为4096。

全连接层3

输入为上一层的输出，输入通道数为4096,输出通道数为1000。

激活函数

VGG中每层使用的激活函数为ReLU激活函数。

由于VGG非常经典，所以，网络上有关于VGG-16、VGG-19预训练的权重，为了为了展示一下每一层的架构，读取VGG-16预训练权重看一下，

import numpy as np

path = "vgg16.npy"
layers = ["conv1_1", "conv1_2",
          "conv2_1", "conv2_2",
          "conv3_1", "conv3_2", "conv3_3",
          "conv4_1", "conv4_2", "conv4_3",
          "conv5_1", "conv5_2", "conv5_3",
          "fc6", "fc7", "fc8"]

data_dict = np.load(path, encoding='latin1').item()

for layer in layers:
    print(data_dict[layer][0].shape)
    
# 输出
(3, 3, 3, 64)
(3, 3, 64, 64)
(3, 3, 64, 128)
(3, 3, 128, 128)
(3, 3, 128, 256)
(3, 3, 256, 256)
(3, 3, 256, 256)
(3, 3, 256, 512)
(3, 3, 512, 512)
(3, 3, 512, 512)
(3, 3, 512, 512)
(3, 3, 512, 512)
(3, 3, 512, 512)
(25088, 4096)
(4096, 4096)
(4096, 1000)

网络共16层，卷积层部分为1*4维的，其中从前到后分别是卷积核高度、卷积核宽度、输入数据通道数、输出数据通道数。

到此为止，应该已经了解了VGG的模型结构，下面就开始使用tensorflow编程实现一下 VGG。

编程实践

因为 VGG非常经典，所以网络上有VGG的预训练权重，我们可以直接读取预训练的权重去搭建模型，这样就可以忽略对输入和输出通道数的感知，要简单很多，但是为了更加清楚的理解网络模型，在这里还是从最基本的部分开始搭建，自己初始化权重和偏差，这样能够更加清楚每层输入和输出的结构。

卷积块

经过前面的介绍应该了解，VGG的主要特点就在于卷积块的使用，因此，我们首先来完成卷积块部分的编写。在完成一段代码的编写之前，我们应该首先弄明白两点：输入和输出。

输出当然很明确，就是经过每个卷积块(多个卷积层)卷积、激活后的tensor，我们要明确的就是应该输入哪些参数？

最重要的3个输入：要进行运算的tensor、每个卷积块内卷积层的个数、输出通道数。

当然，我们为了更加规范的搭建模型，也需要对每一层规定一个命名空间，这样还需要输入每一层的名称。至于输入通道数，我们可以通过tensorflow的get_shape函数获取，

def conv_block(self, X, num_layers, block_index, num_channels):
    in_channels = int(X.get_shape()[-1])
    for i in range(num_layers):
        name = "conv{}_{}".format(block_index, i)
        with tf.variable_scope(name) as scope:
            weight = tf.get_variable("weight", [3, 3, in_channels, num_channels])
            bias = tf.get_variable("bias", [num_channels])
        conv = tf.nn.conv2d(X, weight, strides=[1, 1, 1, 1], padding="SAME")
        X = tf.nn.relu(tf.nn.bias_add(conv, bias))
        in_channels = num_channels
        print(X.get_shape())
    return X

从代码中可以看出，有几个参数是固定的：

卷积窗口大小
步长
填充方式
激活函数

到此为止，我们就完成了VGG最核心一部分的搭建。

池化层

之前看过前两篇关于AlexNet、LeNet的同学应该记得，池化层有两个重要的参数：窗口大小、步长。由于在VGG中这两个超参数是固定的，因此，不用再作为函数的入参，直接写在代码中即可。

def max_pool(self, X):
    return tf.nn.max_pool(X, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")

全连接层

至于全连接层，和前面介绍的两个模型没有什么区别，我们只需要知道输出通道数即可，每一层的输出为上一层的输出，

def full_connect_layer(self, X, out_filters, name):
    in_filters = X.get_shape()[-1]
    with tf.variable_scope(name) as scope:
        w_fc = tf.get_variable("weight", shape=[in_filters, out_filters])
        b_fc = tf.get_variable("bias", shape=[out_filters], trainable=True)
    fc = tf.nn.xw_plus_b(X, w_fc, b_fc)
    return tf.nn.relu(fc)

由于不同网络模型之前主要的不同之处就在于模型的结构，至于训练和验证过程中需要的准确率、损失函数、优化函数等都大同小异，在前两篇文章中已经实现了训练和验证部分，所以这里就不再赘述。在本文里，我使用numpy生成一个随机的测试集测试一下网络模型是否搭建成功即可。

测试

首先使用numpy生成符合正态分布的随机数，形状为(5, 224, 224, 3)，5为批量数据的大小，244为输入图像的尺寸，3为输入图像的通道数，设定输出类别数为1000，

def main():
    X = np.random.normal(size=(5, 224, 224, 3))
    images = tf.placeholder("float", [5, 224, 224, 3])
    vgg = VGG(1000)
    writer = tf.summary.FileWriter("logs")
    with tf.Session() as sess:
        model = vgg.create(images)
        sess.run(tf.global_variables_initializer())
        writer.add_graph(sess.graph)
        prob = sess.run(model, feed_dict={images: X})
        print(sess.run(tf.argmax(prob, 1)))

# 输出
(5, 224, 224, 64)
(5, 224, 224, 64)
(5, 112, 112, 128)
(5, 112, 112, 128)
(5, 56, 56, 256)
(5, 56, 56, 256)
(5, 56, 56, 256)
(5, 28, 28, 512)
(5, 28, 28, 512)
(5, 28, 28, 512)
(5, 14, 14, 512)
(5, 14, 14, 512)
(5, 14, 14, 512)
(5, 4096)
(5, 4096)
(5, 1000)
[862 862 862 862 862]

可以对比看出，每层网络的尺寸和前面加载的预训练模型是匹配的，下面在看一下tensorboard的结果，

$ tensorboard --logdir="logs"

结果，

3.9 GoogLeNet

前言

在前一篇文章介绍VGG时，我提到2014年对于计算机视觉领域是一个丰收的一年，在这一年的ImageNet图像识别挑战赛(ILSVRC,ImageNet Large Scale Visual Recognition Challenge)中出现了两个经典、影响至深的卷积神经网络模型，其中第一名是GoogLeNet、第二名是VGG。

没错，本文的主角就是2014年ILSVRC的第一名--GoogLeNet(Going Deeper with Convolutions)，要注意的是，这个网络模型的名称是"GoogLeNet"，而不是"GoogleNet"，虽然只有一个大小写字母的却别，含义却不同，GoogLeNet之所以叫做这个名字，主要是为了想LeNet致敬。

GoogLeNet与VGG出现在同一年，二者自然有一些相似之处，但是两个模型更多的是差异性。

首先说一下GoogLeNet与VGG的相同之处：

都提出了基础块的思想
均是为了克服网络逐渐变深带来的问题

首先，说一下第一点--都提出了基础块的思想。

前文已经介绍了，VGG使用块代替层的思想，这使得VGG在迁移性方面表现非常好，也因此得到了广泛的应用。而GoogLeNet也使用了基础块的思想，它引入了Inception块，想必说到这里应该接触过深度计算机视觉的同学应该恍然大悟，也许对GoogLeNet的概念已经变的模糊，但是Inception却如雷贯耳，目前在很多CNN模型中同样作为基础模块使用。

其次，说一下第二点--均是为了克服网络逐渐变深带来的问题。

随着卷积神经网络模型的更新换代，我们发现网络层数逐渐变多，模型变的越来越深，这是因为提升模型效果最为直接有效的方法就是增加网络深度和宽度，但是，随着网络层数的加深、加宽，它也会带来很多负面影响，

参数数量增加
梯度消失和梯度爆炸
计算复杂度增加

因此，从VGG、GoogLeNet开始，包括后面会讲到的ResNet，研究者逐渐把目光聚焦在"如何在增加网络深度和宽度的同时，避免上述这些弊端？"

不同的网络模型所采取的方式不同，这也就引出了VGG与GoogLe的不同之处，

输出层不同
克服网络加深弊端的方式不同

首先，说一下第一点--输出层不同，

VGG是在LeNet、AlexNet的基础上引入了基础块的思想，但是在网络架构、输出等放并没有进行太多的改变，在输出层方面同样是采用连续三个全连接层，全连接层的输入是前面卷积层的输出经过reshape得到。

虽然GoogLeNet是向LeNet致敬，但是在GoogLeNet的身上却很难看到LeNet和AlexNet的影子，它的输出更是采用NiN的思想(Network in Network)，它把全连接层编程了1*1的卷积层。

其次，说一下第二点--克服网络加深弊端的方式不同，

VGG在克服网络加深带来的问题方面采用的是引入基础块的思想，但是整体上还是偏向于"更深"，而GoogLeNet更加偏重于"更宽"，它引入了并行网络结构的思想，每一层有4个不同的线路对输入进行处理，然后再块的输出部分在沿着通道维进行连接。

GoogLeNet通过对模型的大幅度改进，使得它在参数数量、计算资源方面要明显优于VGG，但是GoogLeNet的模型复杂度相对于VGG也要高一些，因此，在迁移性方面VGG要优于GoogLeNet。

GoogLeNet模型

Inception块是GoogLeNet模型中一个非常重要的组成部分，因此，在介绍完整的GoogLeNet模型之前，我先来讲解一下Inception块的结构。

Inception块

上图就是就是Inception的结构，Inception分为两个版本：

简化版
降维版

二者主要的区别就在于1*1的卷积层，降维版在第2、3、4条线路添加了1*1的卷积层来减少通道维度，以减小模型复杂度，本文就以降维版为例来讲解GoogLeNet。

现在来看一下Inception的结构，可以很清楚的看出，它包含4条并行线路，其中，第1、2、3条线路分别采用了1*1、3*3、5*5，不同的卷积核大小来对输入图像进行特征提取，使用不同大小卷积核能够充分提取图像特征。其中，第2、3两条线路都加入了1*1的卷积层，这里要明确一点，第2、3两条线路的1*1与第1条线路1*1的卷积层的功能不同，第1条线路是用于特征提取，而第2、3条线路的目的是降低模型复杂度。第4条线路采用的不是卷积层，而是3*3的池化层。最后，4条线路通过适当的填充，使得每一条线路输出的宽和高一致，然后经过Filter Concatenation把4条线路的输出在通道维进行连接。

上述就是Inception块的介绍，在GoogLeNet模型中，Inception块会被多次用到，下面就开始介绍GoogLeNet的完整模型结构。

GoogLeNet

GoogLeNet在网络模型方面与AlexNet、VGG还是有一些相通之处的，它们的主要相通之处就体现在卷积部分，

AlexNet采用5个卷积层
VGG把5个卷积层替换成5个卷积块
GoogLeNet采用5个不同的模块组成主体卷积部分

上述就是GoogLeNet的结构，可以看出，和AlexNet统一使用5个卷积层、VGG统一使用5个卷积块不同，GoogLeNet在主体卷积部分是卷积层与Inception块混合使用。另外，需要注意一下，在输出层GoogleNet采用全局平均池化，得到的是高和宽均为1的卷积层，而不是通过reshape得到的全连接层。

下面就来详细介绍一下GoogLeNet的模型结构。

模块1

第一个模块采用的是一个单纯的卷积层紧跟一个最大池化层。

卷积层：卷积核大小7*7，步长为2，输出通道数64。

池化层：窗口大小3*3，步长为2，输出通道数64。

模块2

第二个模块采用2个卷积层，后面跟一个最大池化层。

卷积层：卷积核大小3*3，步长为1，输出通道数192。

池化层：窗口大小3*3，步长为2，输出通道数192。

模块3

第三个模块采用的是2个串联的Inception块，后面跟一个最大池化层。

第一个Inception的4条线路输出的通道数分别是64、128、32、32，输出的总通道数是4条线路的加和，为256。

第二个Inception的4条线路输出的通道数分别是128、192、96、64，输出的总通道数为480。

池化层：窗口大小3*3，步长为2，输出通道数480。

模块4

第4个模块采用的是5个串联的Inception块，后面跟一个最大池化层。

第一个Inception的4条线路输出的通道数分别是192、208、48、64，输出的总通道数为512。

第二个Inception的4条线路输出的通道数分别是160、224、64、64，输出的总通道数为512。

第三个Inception的4条线路输出的通道数分别是128、256、64、64，输出的总通道数为512。

第四个Inception的4条线路输出的通道数分别是112、288、64、64，输出的总通道数为528。

第五个Inception的4条线路输出的通道数分别是256、320、128、128，输出的总通道数为832。

池化层：窗口大小3*3，步长为2，输出通道数832。

模块5

第五个模块采用的是2个串联的Inception块。

第一个Inception的4条线路输出的通道数分别是256、320、128、128，输出的总通道数为832。

第二个Inception的4条线路输出的通道数分别是384、384、128、128，输出的总通道数为1024。

输出层

前面已经多次提到，在输出层GoogLeNet与AlexNet、VGG采用3个连续的全连接层不同，GoogLeNet采用的是全局平均池化层，得到的是高和宽均为1的卷积层，然后添加丢弃概率为40%的Dropout，输出层激活函数采用的是softmax。

激活函数

GoogLeNet每层使用的激活函数为ReLU激活函数。

编程实践

当我们拿到一个需求的时候，应该先对它进行一下分析、分解，针对GoogLeNet，我们通过分析可以把它分解成如下几个模块，

Inception块
卷积层
池化层
线性层

通过上述分解，我们逐个来实现上述每个模块。

Inception块

前面讲解过程中已经详细介绍Inception块的结构，它包括4条线路，而对于Inception块最重要的参数就是每个线路输出的通道数，由于其中步长、填充方式、卷积核大小都是固定的，因此不需要我们进行传参。我们把4条线路中每层的输出通道数作为Inception块的入参，具体实现过程如下，

def inception_block(X, c1, c2, c3, c4, name):
    in_channels = int(X.get_shape()[-1])
    # 线路1
    with tf.variable_scope('conv1X1_{}'.format(name)) as scope:
        weight = tf.get_variable("weight", [1, 1, in_channels, c1])
        bias = tf.get_variable("bias", [c1])
    p1_1 = tf.nn.conv2d(X, weight, strides=[1, 1, 1, 1], padding="SAME")
    p1_1 = tf.nn.relu(tf.nn.bias_add(p1_1, bias))

    # 线路2
    with tf.variable_scope('conv2X1_{}'.format(name)) as scope:
        weight = tf.get_variable("weight", [1, 1, in_channels, c2[0]])
        bias = tf.get_variable("bias", [c2[0]])
    p2_1 = tf.nn.conv2d(X, weight, strides=[1, 1, 1, 1], padding="SAME")
    p2_1 = tf.nn.relu(tf.nn.bias_add(p2_1, bias))
    p2_shape = int(p2_1.get_shape()[-1])
    with tf.variable_scope('conv2X2_{}'.format(name)) as scope:
        weight = tf.get_variable("weight", [3, 3, p2_shape, c2[1]])
        bias = tf.get_variable("bias", [c2[1]])
    p2_2 = tf.nn.conv2d(p2_1, weight, strides=[1, 1, 1, 1], padding="SAME")
    p2_2 = tf.nn.relu(tf.nn.bias_add(p2_2, bias))

卷积及池化

在GoogLeNet中多处用到了卷积层和最大池化层，这些结构在AlexNet中都已经实现过，我们直接拿过来使用即可，

def conv_layer(self, X, ksize, out_filters, stride, name):
    in_filters = int(X.get_shape()[-1])
    with tf.variable_scope(name) as scope:
        weight = tf.get_variable("weight", [ksize, ksize, in_filters, out_filters])
        bias = tf.get_variable("bias", [out_filters])
    conv = tf.nn.conv2d(X, weight, strides=[1, stride, stride, 1], padding="SAME")
    activation = tf.nn.relu(tf.nn.bias_add(conv, bias))
    return activation

def pool_layer(self, X, ksize, stride):
    return tf.nn.max_pool(X, ksize=[1, ksize, ksize, 1], strides=[1, stride, stride, 1], padding="SAME")

线性层

GoogLeNet与AlexNet、VGG在输出层不同，AlexNet和VGG是通过连续的全连接层处理，然后输入到激活函数即可，而GoogLeNet需要进行全局平均池化后进行一次线性映射，对于这一点实现过程如下，

def linear(self, X, out_filters, name):
    in_filters = X.get_shape()[-1]
    with tf.variable_scope(name) as scope:
        w_fc = tf.get_variable("weight", shape=[in_filters, out_filters])
        b_fc = tf.get_variable("bias", shape=[out_filters], trainable=True)
    fc = tf.nn.xw_plus_b(X, w_fc, b_fc)
    return tf.nn.relu(fc)

搭建模型

上面几步已经把GoogLeNet主要使用的组件已经搭建完成，接下来要做的就是把它们组合到一起即可。这里需要注意一点，全局平均池化层的填充方式和前面卷积层、池化层使用的不同，这里需要使用VALID填充方式，

def create(self, X):
    # 模块1
    module1_1 = self.conv_layer(X, 7, 64, 2, "module1_1")
    pool_layer1 = self.pool_layer(module1_1, 3, 2)

    # 模块2
    module2_1 = self.conv_layer(pool_layer1, 1, 64, 1, "modul2_1")
    module2_2 = self.conv_layer(module2_1, 3, 192, 1, "module2_2")
    pool_layer2 = self.pool_layer(module2_2, 3, 2)

    # 模块3
    module3a = self.inception_block(pool_layer2, 64, (96, 128), (16, 32), 32, "3a")
    module3b = self.inception_block(module3a, 128, (128, 192), (32, 96), 64, "3b")
    pool_layer3 = self.pool_layer(module3b, 3, 2)

    # 模块4
    module4a = self.inception_block(pool_layer3, 192, (96, 208), (16, 48), 64, "4a")
    module4b = self.inception_block(module4a, 160, (112, 224), (24, 64), 64, "4b")
    module4c = self.inception_block(module4b, 128, (128, 256), (24, 64), 64, "4c")
    module4d = self.inception_block(module4c, 112, (144, 288), (32, 64), 64, "4d")
    module4e = self.inception_block(module4d, 256, (160, 320), (32, 128), 128, "4e")
    pool_layer4 = self.pool_layer(module4e, 3, 2)

    # 模块5
    module5a = self.inception_block(pool_layer4, 256, (160, 320), (32, 128), 128, "5a")
    module5b = self.inception_block(module5a, 384, (192, 384), (48, 128), 128, "5b")

    pool_layer5 = tf.nn.avg_pool(module5b, ksize=[1, 7, 7, 1], strides=[1, 1, 1, 1], padding="VALID")
    flatten = tf.reshape(pool_layer5, [-1, 1024])
    dropout = tf.nn.dropout(flatten, keep_prob=self.keep_prob)
    linear = self.linear(dropout, self.num_classes, 'linear')
    return tf.nn.softmax(linear)

验证

为了验证每一个模块输出的形状和原文中给出的是否一致，我使用numpy，生成了样本数为5的随机样本，看一下每一层的输出结果，

def main():
    X = np.random.normal(size=(5, 224, 224, 3))
    images = tf.placeholder("float", [5, 224, 224, 3])
    googlenet = GoogLeNet(1000, 0.4)
    writer = tf.summary.FileWriter("logs")
    with tf.Session() as sess:
        model = googlenet.create(images)
        sess.run(tf.global_variables_initializer())
        writer.add_graph(sess.graph)
        prob = sess.run(model, feed_dict={images: X})
        print(sess.run(tf.argmax(prob, 1)))
        
# 输出
module1_1:      (5, 112, 112, 64)
pool_layer1:    (5, 56, 56, 64)
module2_1:      (5, 56, 56, 64)
module2_2:      (5, 56, 56, 192)
pool_layer2:    (5, 28, 28, 192)
module3a:       (5, 28, 28, 256)
module3b:       (5, 28, 28, 480)
pool_layer3:    (5, 14, 14, 480)
module4a:       (5, 14, 14, 512)
module4b:       (5, 14, 14, 512)
module4c:       (5, 14, 14, 512)
module4d:       (5, 14, 14, 528)
module4e:       (5, 14, 14, 832)
pool_layer4:    (5, 7, 7, 832)
module5a:       (5, 7, 7, 832)
module5b:       (5, 7, 7, 1024)
pool_layer5:    (5, 1, 1, 1024)
flatten:        (5, 1024)
linear:         (5, 1000)

可以从上述输出可以看出，每一层的输出形状和原文中给出的一致，至于在不同场景、不同数据集下的表现效果，这需要针对性的进行调优。

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

PyHubWeekly

序言

第一章数字图像处理

1.1 图像预处理之图像去噪

1.2 图像预处理之图像增强

1.3 图像预处理之图像分割

1.4 图像预处理之图像增广

第二章传统目标检测

2.1 特征工程

2.2 Harris角点检测

2.3 SIFT特征

2.4 HOG特征

2.5 DPM模型

第三章卷积神经网络

3.1 卷积神经网络综述

3.2 卷积层、池化层与填充

3.3 激活函数

3.4 批量归一化

3.5 Dropout

3.6 LeNet

3.7 AlexNet

3.8 VGG

3.9 GoogLeNet

Files

README.md

Latest commit

History

README.md

File metadata and controls

PyHubWeekly

序言

第一章 数字图像处理

1.1 图像预处理之图像去噪

1.2 图像预处理之图像增强

1.3 图像预处理之图像分割

1.4 图像预处理之图像增广

第二章 传统目标检测

2.1 特征工程

2.2 Harris角点检测

2.3 SIFT特征

2.4 HOG特征

2.5 DPM模型

第三章 卷积神经网络

3.1 卷积神经网络综述

3.2 卷积层、池化层与填充

3.3 激活函数

3.4 批量归一化

3.5 Dropout

3.6 LeNet

3.7 AlexNet

3.8 VGG

3.9 GoogLeNet

第一章数字图像处理

第二章传统目标检测

第三章卷积神经网络