$k$ 均值聚类算法(k-means clustering algorithm) 在聚类的问题中,我们得到了一组训练样本集 ${x^{(1)},...,x^{(m)}}$ ,然后想要把这些样本划分成若干个相关的“类群(clusters)”。其中的 $x^{(i)}\in R^n$ ,而并未给出分类标签 $y^{(i)}$ 。所以这就是一个无监督学习的问题了。
$K$ 均值聚类算法如下所示:
随机初始化(initialize)聚类重心(cluster centroids) $\mu_1, \mu_2,..., \mu_k\in R^n$ 。
重复下列过程直到收敛(convergence): {
对每个 $i$ ,设
$$
c^{(i)}:=arg\min_j||x^{(i)}-\mu_j||^2
$$
对每个 $j$ ,设
$$
\mu_j:=\frac{\sum_{i=1}^m1{c^{(i)}=j}x^{(i)}}{\sum_{i=1}^m1{c^{(i)}=j}}
$$
}
在上面的算法中,$k$ 是我们这个算法的一个参数,也就是我们要分出来的群组个数(number of clusters);而聚类重心 $\mu_j$ 表示的是我们对各个聚类的中心位置的当前猜测。在上面算法的第一步当中,需要初始化(initialize)聚类重心(cluster centroids),可以这样实现:随机选择 $k$ 个训练样本,然后设置聚类重心等于这 $k$ 个样本 各自的值。(当然也还有其他的初始化方法。)
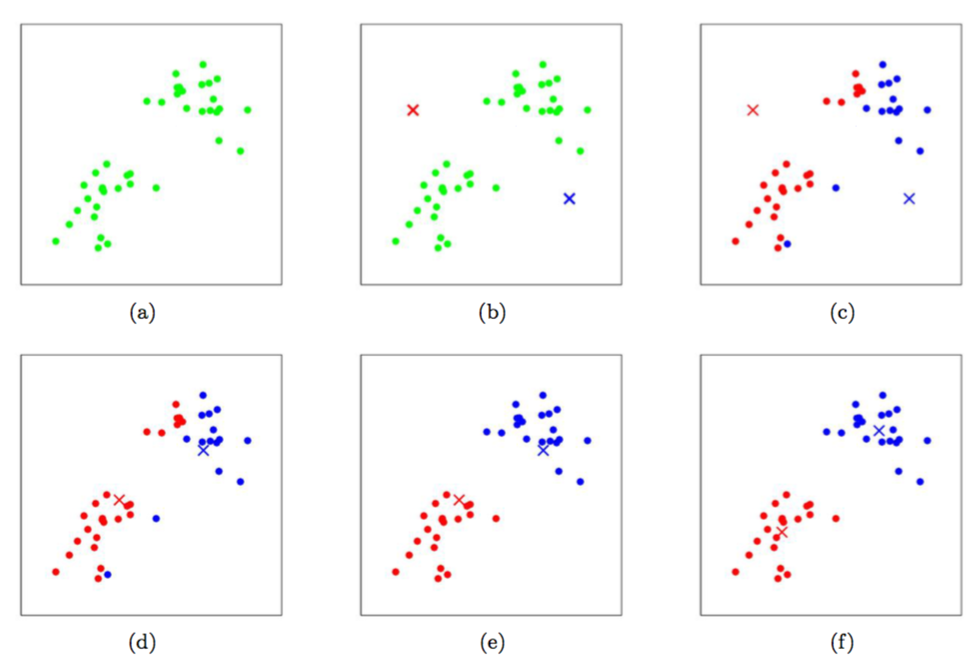
算法的第二步当中,循环体内重复执行两个步骤:(i)将每个训练样本$x^{(i)}$ “分配(assigning)”给距离最近的聚类重心$\mu_j$;(ii)把每个聚类重心$\mu_j$ 移动到所分配的样本点的均值位置。下面的 图1 就展示了运行 $k$ 均值聚类算法的过程。
图1:$k$ 均值聚类算法。图中的圆形点表示的是训练样本,交叉符号表示的是聚类重心。(a) 原始训练样本数据集。 (b) 随机初始化的聚类重心(这里的初始化方法就跟我们上面说的不一样,并没有从训练样本中选择两个点)。(c-f) 运行 $k$ 均值聚类算法中的两步迭代的示意图。在每一次迭代中,我们把每个训练样本分配给距其最近的聚类重心(用同样颜色标识出),然后把聚类重心移动到所分配的样本的均值位置。(用颜色区分效果最好了。)图片引用自 Michael Jordan。
$K$ 均值聚类算法能保证收敛性么?可以的,至少在一定意义上能这么说。尤其是我们可以定义一个下面这样的函数作为失真函数(distortion function):
$$
J(c,\mu)=\sum_{i=1}^m ||x^{(i)}-\mu_{c^{(i)}}||^2
$$
这样就可以用 $J$ 来衡量每个样本 $x^{(i)}$ 和对应的聚类重心$\mu_{c^{(i)}}$之间距离的平方和。很明显能看出 $k$ 均值聚类算法正好就是对 $J$ 的坐标下降过程。尤其是内部的循环体中,$k$ 均值聚类算法重复对 $J$ 进行最小化,当 $\mu$ 固定的时候用 $c$ 来最小化 $J$ ,当 $c$ 固定的时候则用 $\mu$ 最小化 $J$ 。这样就保证了 $J$ 是单调降低的(monotonically decrease),它的值也就必然收敛(converge)。(通常这也表明了 $c$ 和 $\mu$ 也收敛。在理论上来讲,$k$均值 可能会在几种不同的聚类之间摆动(oscillate),也就是说某些组不同值的 $c$ 和/或 $\mu$ 对应有完全相同的 $J$ 值,不过在实践中这种情况几乎不会遇到。)
失真函数 $J$ ,是一个非凸函数(non-convex function),所以对 $J$ 进行坐标下降(coordinate descent)并不一定能够收敛到全局最小值(global minimum)。也就是说,$k$ 均值聚类算法可能只是局部最优的(local optima)。通常除了这个问题之外,$k$ 均值聚类效果都不错,能给出很好的聚类。如果你担心陷入到某些比较差的局部最小值,通常可以多次运行 $k$ 均值距离(使用不同的随机值进行来对聚类重心 $\mu_j$ 进行初始化)。然后从所有的不同聚类方案(clusterings)中,选择能提供最小失真(distortion) $J(c,\mu)$ 的。