homework_06_spheres_v

Spheres V

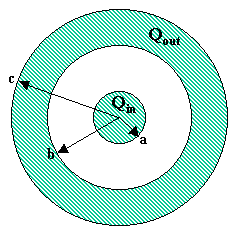
A solid metal sphere of radius [a = 2.5 cm] has a net charge [Q_{in} = - 3.0 n C]. The sphere is surrounded by a concentric conducting spherical shell of inner radius [b = 6.0 cm] and outer radius [c = 9.0 cm]. The shell has a net charge [Q_{out} = [+ 2.0 nC]. What is [V_0], the electric potential at the center of the metal sphere, given the potential at infinity is zero?

• Given

  • [\vec E( r) = -\frac{ d v}{ d r} \hat r ]
  • [ \vec E = k \frac{ Q}{ r^2}]

• Let

  • [a = 2.5 cm = .025 m]
  • [b = 6.0 cm = .06 m]
  • [c = 9.0 cm = .09 m]
  • [Q_{in} = - 3.0 n C]
  • [Q_{out} = 2 n C]

• [V = -\left( \int\limits_{\infty}^{c}{ \vec E \cdot d \vec l} \int\limits_{c}^{b}{ \vec E \cdot d \vec l} \int\limits_{b}^{a}{ \vec E \cdot d \vec l} \int\limits_{a}^{0}{ \vec E \cdot d \vec l}\right) ]

• [V = -\left( \int\limits_{\infty}^{c}{ \vec E \cdot d \vec l} \int\limits_{b}^{a}{ \vec E \cdot d \vec l}\right)]

  • [\int\limits_{c}^{b}{ \vec E \cdot d \vec l} = 0]
  • [\int\limits_{a}^{0}{ \vec E \cdot d \vec l} = 0]

• [V = -\left( \int\limits_{\infty}^{c}{ k \frac{ Q_{out}}{ r^2} dr} \int\limits_{b}^{a}{ k \frac{ Q_{in}}{ r^2} dr}\right)]

• Hints

  • [V = kQ/r] cannot be used directly here. We need to start with an expression for [V] which is always true.
    • Despite the spherical symmetery, since we are interested in the potential inside the charge distribution, we cannot use [V = k \frac{ Q}{ r}].
  • Coulomb's law is always true, but the calculation would be difficult for this problem. We can use the spherical symmetry to significantly reduce our work.
  • The spherical symmetry of the problem lets us use the result from Gauss' law. [E = k \frac{ Q_{enclosed}}{ r_2}]
  • Divid the problem in four seperate regions
    • Inside the sphere [r < a]
    • Between the sphere and the shell [a < r < b]
    • Inside the sphereical shell [b < r < c]
    • Outside the spherical shell [r > c]
  • Determine the potential at the origin you need to evaluate
    • [V = -\left( \int\limits_{\infty}^{c}{ \vec E \cdot d \vec l} \int\limits_{c}^{b}{ \vec E \cdot d \vec l} \int\limits_{b}^{a}{ \vec E \cdot d \vec l} \int\limits_{a}^{0}{ \vec E \cdot d \vec l}\right) ]

• [V_0 =]