q02b

q02b

• [F_{ij} = \kappa \frac{ q_i q_j}{ r^2} \hat r]
  • [ \kappa = \frac{ 1}{ 4 \pi \epsilon_0} = 8.99 \times 10^9 \frac{ Nm^2}{ C^2} ]
  • [ \mu = 10^{-6}]
• Let:
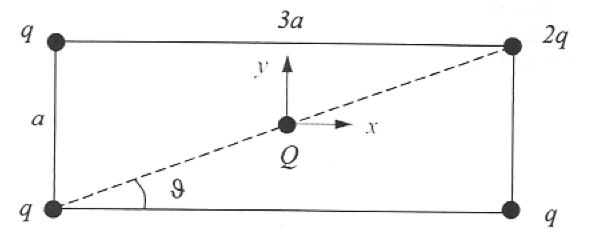
  • [ a ] be the height of the rectangle
  • [ 3a ] be the lenght of the rectangle
  • [ d = \sqrt{ a^2 + (3a)^2 }]
  • [ \theta = \arctan{ \left( \frac{ \frac{ a}{ 2}}{ \frac{ 3a}{ 2}}\right)}]

(a)

• [ F_Q = \kappa \frac{ q Q}{ \left(\frac{ d}{ 2} \right)^2} ]

(b)

• [ \sin{ (\theta)} = \frac{ \frac{ a}{ 2}}{ \frac{ d}{ 2}} ]
• [ \cos{ (\theta)} = \frac{ \frac{ 3a}{ 2}}{ \frac{ d}{ 2}} ]
• [ \tan{ (\theta)} = \frac{ \frac{ a}{ 2}}{ \frac{ 3a}{ 2}} ]

(c)

• [ F_{Q,x} = \kappa \frac{ q}{ \frac{ d}{ 2}} \cos{ (\theta)} ]
• [ F_{Q,y} = \kappa \frac{ q}{ \frac{ d}{ 2}} \sin{ (\theta)} ]

(d)

• Let:
  • [ q = 3 \mu C ]
  • [ a = .02 m ]
• Then:
  • [ d = \sqrt{ a^2 + (3a)^2 } = 0.063246]
• [ F_Q = \kappa \frac{ q}{ \left(\frac{ d}{ 2} \right)^2} = 2.697 \times 10^7 ]

(e)

• Let:
  • [ q = 3 \mu C ]
  • [ Q = 4 \mu C ]
  • [ a = .02 m ]
• Then:
  • [ d = \sqrt{ a^2 + (3a)^2 } = 0.063246]
• [ F_Q = \kappa \frac{ q Q}{ \left(\frac{ d}{ 2} \right)^2} = 107.88 ]