prelecture_14_biot savart_law
- Until now, we have taken magnetic fields to be a given
- Now, we will examine how magnetic fields are created
- Magnetic fields are produced by electric currents
- We can calculate magnetic fields produced by current distrobutions using the Biot-Savart Law
- Start, by examining the magnetic field produced by an infinite current carrying wire.
- Next, we use the result we found to examine the forces exerted
by parallel current carrying wires
- Finally, we calculate the magnetic field along the axis of a
circular current carrying loop.
- [d \vec B = \frac{ \mu_0 I}{ 4 \pi} \frac{ d \vec s \times \hat r}{ r^2}]
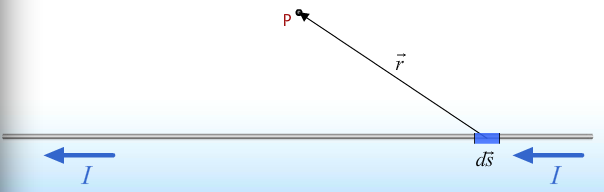
- The magnetic field [d \vec B] that is produced by current [I] in a segment of length [d \vec s] at a point that is a distance [\vec r] from the segment is given by the above expression.
- [\mu_0 = 4 \pi \times 10^{-7} \frac{ T \cdot m}{ A}]
- [\frac{ T \cdot m}{ A} \Rightarrow] Tesla metters per aplitude.
- Direction of [d \vec S] is in that of the current, the direction of the positive charge
- [\vec r] is a vector from the segment to the point at which we want to determine the magnetic field.
- Direction of the magnetic field is determined by [d \vec s \times \hat r]
- Right hand rule
- Fingers point in direction of [d \vec s]
- Curl fingers toward [\vec r]
- Thumb gives direction of [d \vec B]
- For the case in the image above the direction of the magnetic field is into the screen.
- Right hand rule
- [B = \frac{ \mu_0 I}{ 2 \pi R}]
- [\vec B = \int d \vec B = \frac{ \mu_0 I}{ 4 \pi} \int \frac{ d \vec s \times \hat r}{ r^2}]
- Biot-Savart Law
-
- [r = \frac{ R}{ \cos \alpha}]
- [x = R \tan \alpha]
- [ds = dx = \frac{ R}{ \cos^2 \alpha} d \alpha]
- For all segment the magnetic fiel is out of the screen
- [\vec B = \frac{ \mu_0 I}{ 4 \pi} \int \frac{ d \vec s \times \hat r}{ r^2}]
- [= \frac{ \mu_0 I}{ 4 \pi} \int \frac{ \sin \theta ds}{ r^2} \hat z]
- [= \frac{ \mu_0 I}{ 4 \pi} \int\limits_{-\frac{ \pi}{ 2}}^{\frac{ \pi}{ 2}}{ \frac{ \cos \alpha}{ r^2} \frac{ R}{ \cos^2 \alpha} d \alpha \hat z}]
- [= \frac{ \mu_0 I}{ 4 \pi} \int\limits_{-\frac{ \pi}{ 2}}^{\frac{ \pi}{ 2}}{ \frac{ \cos \alpha}{ \left(\frac{ R}{ \cos \alpha}\right)^2} \frac{ R}{ \cos^2 \alpha} d \alpha \hat z}]
- [= \frac{ \mu_0 I}{ 4 \pi} \int\limits_{-\frac{ \pi}{ 2}}^{\frac{ \pi}{ 2}}{ \cos \alpha d \alpha \hat z}]
- [= \frac{ \mu_0 I}{ 4 \pi R} 2 = \frac{ \mu_0 I}{ 2 \pi R}]
- [\vec B = \int d \vec B = \frac{ \mu_0 I}{ 4 \pi} \int \frac{ d \vec s \times \hat r}{ r^2}]
- We now want to discuss some of the features of this result for the magnetic field
of an infinite linear current.
- [B = \frac{ \mu_0 I}{ 2 \pi R}]
- The magnitude of the field is proportional to [\frac{ I}{ R}]
- Similar to that of the electric field of an infinite line of charge
- Charge Element [d \vec E = \frac{ 1}{ 4 \pi \varepsilon_0} \frac{ d q}{ r^2} \hat r]
- Current Element [d \vec B = \frac{ \mu_0 I}{ 4 \pi} \frac{ d \vec s \times \hat r}{ r^2}]
- Right Hand Rule
- Place thumb in direction of [I]
- Fingers curl in direction of [B]
The magnitude of the magnetic field at a point a distance [d] to the right of a long straight wire carrying current [i] out of the plane of the page is [B_1] (Case 1 below - the red dot represents the wire). Suppose a second current carrying wire identical to the first is placed the same distance to the right of the point (Case 2 below).
Compare the magnitude of the total magnetic field at the point in Case 2 ([B_2]), with that in Case 1 ([B_1]).
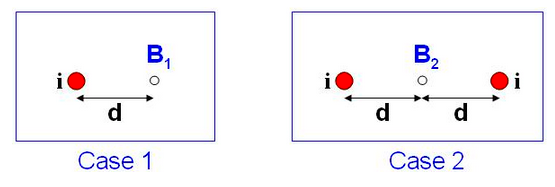
- [B_2 = 0]
- As illustrated in the picture below, the fields from the two identical wires cancel at a point halfway between them. This is easy to understand since the magnitude of the fields from each wire is the same (the currents in the wires and the distance from the wires is the same for both), but directions of the field from the two wires is opposite (using the right hand rule).
- q2a.png-
- [F_2 = F_1 = \frac{ \mu_0}{ 2 \pi d} I_1 I_2 L]
* [\vec F_1 = -\vec F_2]
- Since we know the form of the magnetic field of a long strait wire [B = \frac{ \mu_0 I}{ 2 \pi R}]
- Now we can look at two parallel current carrying wires, we interpret this by looking at the magnetic field produced by each wire.