forked from KurtRudolph/phys212
-
Notifications
You must be signed in to change notification settings - Fork 13
prelecture_11_rc_circuits
Kurt Robert Rudolph edited this page Jul 8, 2012
·
16 revisions
- Last time
- Kirchhoff's Rules
- Voltage Rule [\sum \Delta V_n = 0]
- Current Rule [\sum I_{in} = \sum I_{out}]
- Real Batteries
- [V_b = V_0 \frac{ \frac{ R}{ r}}{ 1 + \frac{ R}{ r}]
- Kirchhoff's Rules
- Today we discuss RC Circuits

- Start with a circuit that charges a battery through a resistor.
- Move on to a circuit that removes the battery so the capacitor is discharged.
- Close by discussing the energy flow in these circuits.
- Simple circuit containing a battery, capacitor and resistor.
- Last time we saw the circuit with just a battery and a capacitor that
- [V_b = V_c]
- [q = C V_C]

- This was viewed as being charged instantaneously after the battery was connected to it.
- We now look at adding a resistor to the circuit.

- This will limit the rate at which charge will flow to the capacitor and hence the rate at which the voltage accross the capacitor is able to be charged.
- We now close the gate and charge begins to flow
- We now try to understand the magnitude and direction of this current
as a function of time.
- Recall the voltage drop accross a capacitor is equal to the charge over it's capacitance. * [V_C = \frac{ q}{ C}]
- Initially the voltage across the capacitor is zero [V_C( 0) = 0]
- At [t = 0] the circuit looks like it only contains a battery and a resistor.
- Hence [I(0) = \frac{ V_b}{ R}]
- As current continues to flow the top plate become positively charged and the bottom
plate becomes negatively charched.
- In turn a non zero voltage develops accross the capacitor.
- This results in a reduced voltage accross the resistor as well.
- By Kirchhoff's voltage rules the sum of the must equal the battery voltage.
- Assentonically the current goes to zero as the charge on the capacitor approaches
it's maximum value.

In our discussion of RC circuits we approached the problem as though current was actually flowing through the capacitor. On the other hand, it seems like the construction of a parallel plate capacitor should not allow actual charge to move across the gap between the plates. How can we explain this apparent paradox?
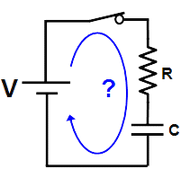
- Charge flows into the top of the capacitor and out of the bottom of the capacitor,
but no charge actually crosses the gap between the plates.
- Charge flows from the positive (top) terminal of the battery to the top plate of the capacitor. Since the battery has to remain neutral at all times, exactly the same amount of charge is pulled from the bottom plate of the capacitor and into the negative (bottom) terminal of the battery. The result is that the top and bottom plates of the capacitor always hold equal and opposite charge, the current is equal in all parts of the circuit, and no actual charge is moving accross the gap of the capacitor.
- We now look the time dependence of the current and the voltage in the circuit.
-

- Moving clockwise around the circuit we find
- [q( t) = C V_b (1 - e^{\frac{ -t}{ R C}})]
- [IR + \frac{ q}{ C} - V_b = 0]
- [R \frac{ d q}{ d t} + \frac{ 1}{ C} q - V_b = 0]
- exponentail function [q( t) \prop e^{-a t}]
- [q( 0) = 0] and [ q( \infty) = C V_b]
- [I( t) = \frac{ V_b}{ R} e^{ -t}{ R C}]
- [I = \frac{ d q}{ d t} = C V_b (-e^{\frac{ -t}{ RC}) \left(-\frac{ 1}{ RC}\right)]
- [I( 0) = \frac{ V_b}{ R}] and [I( \infty) = 0]
- [q( t) = C V_b (1 - e^{\frac{ -t}{ R C}})]
- Moving clockwise around the circuit we find
- We now the switch from position A to position B, removing the battery from the circuit.
-

- Immediately after the switch is moved the charge remains the same,
- [q( 0) = q_0]
- [V_C( 0) = \frac{ q_0}{ C}]
- [q( t) = q_0 e^{\frac{ -t}{ R C}}]
- [I R + \frac{ q}{ C} = 0]
- [\frac{ d q}{ d t} R + \frac{ q}{ C} = 0]
- [q( 0) = q_0] and [q( \infty) = 0]
- [I( t) = -\frac{ q_0}{ R C} e^{\frac{ -t}{ RC}}]
- [I = \frac{ d q}{ d t}]
- [= q_0 e^{ \frac{ -t}{ R C}} \left(-\frac{ 1}{ R C}\right)]
- The positive current flows in the oposite direction to what we originally assumed
- [|I( 0)| = \frac{ q_0}{ RC}] and [I( \infty) = 0]
- Immediately after the switch is moved the charge remains the same,
- [\tau = RC] the time constant of the circuit.
- As we saw in our exponential function for charging and discharging a circuit [e] is dependent on \frac{ -t}{ R C}.
- [q( t) = C V_b (1 - e^{\frac{ -t}{ R C}})]
- [q( t) = q_0 e^{ \frac{ -t}{ R C}}]
- [I( t) = \frac{ V_b}{ R} e^{\frac{ -t}{ R C}}]
- [I( t) = -\frac{ q_0}{ R C} e^{\frac{ -t}{ R C}}]
- As we saw in our exponential function for charging and discharging a circuit [e] is dependent on \frac{ -t}{ R C}.
- Previously we look a circuit with only a resistor where the
rate at which power was being supplied to the system was equal to
that which was being dissipated by the resistor in the form of heat.
-

- [P_{Battery} = P_{Resistor} = I V_b]
-
- Now we will look a circuit with a capacitor.

- [P_{Battery}( t) = P_R( t) + P_C( t)]
- [P_{Battery} = V_b I( t) = V_b I_0 e^{\frac{ -t}{ R C}}]
- [P_R( t) = I^2 R = R I_0^2 e^{\frac{ -2t}{ R C}}]
- The rate at which power is being dissipated by the resistor
- [U_C( t) = \frac{ 1}{ 2} \frac{ q^2}{ C} = \frac{ 1}{ 2} \frac{ q_0^2}{ C} (1 - e^{\frac{ -t}{ RC}})^2] * The rate at which the capacitor is storing power
- [P_C( t) = V_C( t) I( t) = \frac{ q( t)}{ C} I( t) = \left[\frac{ q_0}{ C}(1 - e^{\frac{ -t}{ R C}}\right] \left[I_0 e^{\frac{ -t}{ R C}}\right]]
- We applied Kirchoff's voltage rule as a time dependent differential equation.
- Kirchhoff's Rules
- Voltage Rule [\sum \Delta V_n = 0]
- Current Rule [\sum I_{in} = \sum I_{out}]
- Real Batteries
- [V_b = V_0 \frac{ \frac{ R}{ r}}{ 1 + \frac{ R}{ r}]
- Kirchhoff's Rules
- Next we found these equations were dependent on a time constant [\tau = R C]
- The rate at which energy is being supplied to circuit by the
battery is equal to rate at which the capacitor is storing it
plus the rate at which the resistor is dissipating it.
- [P_{Battery}( t) = P_R( t) + P_C( t)]
